对于非比例电路，我们必须假设完整的电阻容差，因为容差不会分开。我们可以将输出电压计算为 V OUT =IR，其中 I 是理想的 1mA 电流源，R 是 5% 的电阻器（图 1a）。V OUT =1 mA （1±0.05±0.05）1 kΩ=（1±0.05±0.05）V。V OUT的范围是 0.9V≤V OUT ≤1.1V，但我们可以通过使用另一个电阻器调整初始容差来缩小范围（图 1b）。

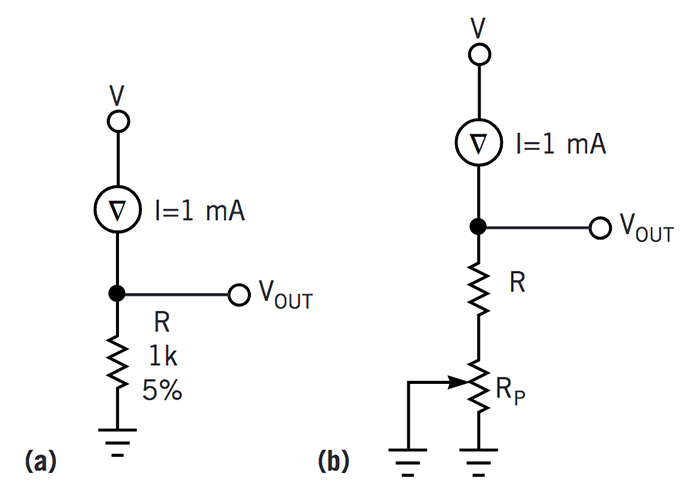
　　图 1非比率电路必须假设完整的电阻容差，因为容差不会分开。基本计算很简单（a），我们可以通过添加另一个电阻来缩小范围以调整初始容差误差（b）。

　　我们可以计算可调电阻值 R P，如下所示：

　　1.

　　为 R 选择最接近的十进制值，该值小于 R=0.9 kΩ 的最小计算值；该值为 R=0.82 kΩ。

　　2.

　　3.

　　计算所选电阻的最小值如下：R MIN =（1–P–D）R=0.9（0.82）=0.738 kΩ。

　　4.

　　5.

　　可变电阻 R P必须弥补 R MIN和 1 kΩ 之间的差值，因此 R PMIN =1–0.738=0.262 kΩ。

　　6.

　　7.

　　电位器的容差可能相当高，因此 R P =R PMIN /（1–T）=0.262 kΩ/（1–D–P）=0.262/0.8=0.328 kΩ。

　　8.

　　9.

　　选择 R P =500Ω。

　　10.

　　最终值为 R=820Ω 和 R P =500Ω。一些工程师认为，最坏情况的设计程序过于严格，并迫使电位器值较大、分辨率较低和电位器漂移误差较大。此问题的一种可能解决方案是降低电位器值并冒险，但更好的解决方案是使用精度更高的部件。非比率电路必须考虑全公差摆动；因此，5% 的采购容差会导致 20% （±10%） 的总体容差。

　　比例电路

　　图 2和公式 1的分压器是经典的比例电路。参考公差方程，我们可以看到公差的某些部分超出了方程。

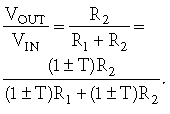
　　公式 1

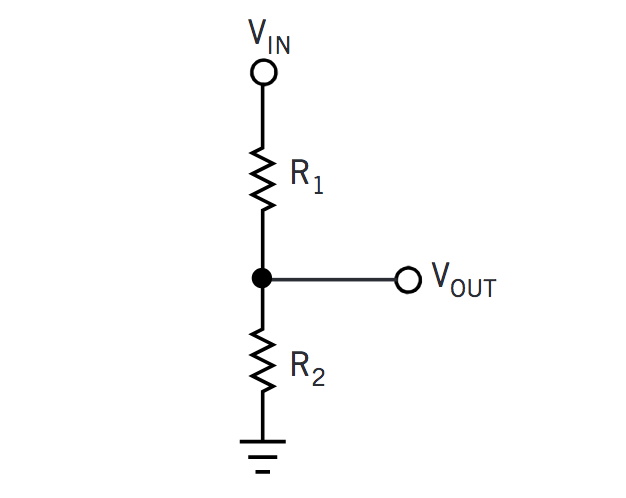
　　图 2比率电路划分了电阻值的一些容差。

　　为获得最大增益值，我们将容差设置为 R 2高和 R 1低。因为 R 2的公差很高，所以它在等式的所有部分都显示为 （1+T）R 2 。表 2列出了四种电阻比的理想增益、最大增益和百分比误差。请注意，最小增益误差发生在 R 1 =R 2时，并且该增益误差等于容差。非比率电路必须接受两倍的容差或 2T，但比率电路可以只有 T 的容差。

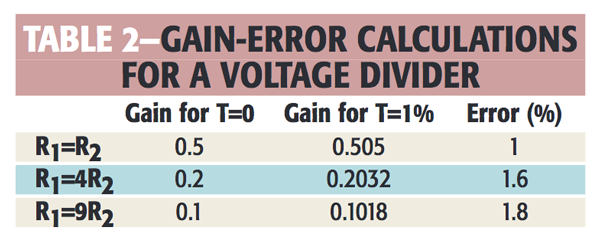
　　当分压器中的两个电阻器容差同时高或低时，容差就会分开。当电阻器制造商保证所有电阻器在环境温度变化期间按比例并沿相同方向漂移时，温度容差就会分出。

　　差分放大器：独立

　　许多参考资料表明，我们无法使用分立部件构建具有良好 CMR（共模抑制）的精密差分放大器。差分放大器的这种容差分析解释了为什么这种说法是正确的。考虑图 3和公式 2（参考文献 1）中的差分放大器电路，并假设放大器是完美的。

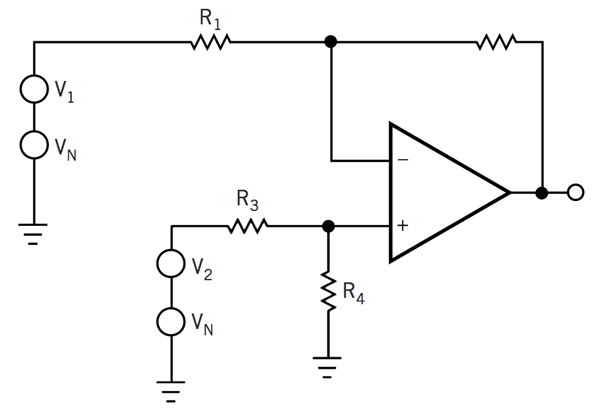
　　图 3差分放大器使用比率电阻器来获得高 CMR。

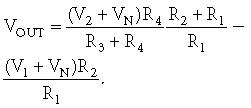
　　公式 2

　　电路 CMR 是在没有信号的情况下测量的，因此 V 1 =V 2 =0.0，公式 2变为公式 3：

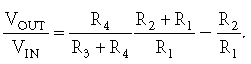
　　公式 3

　　当R 1 =R 3且R 2 =R 4时，增益变为零，CMR 为无限大。实际上，电阻器容差和运算放大器误差总是将 CMR 限制在大约 100 dB 或更低。将等式 3重写为等式 4将我们的注意力集中在差分增益和电阻器容差上。等式 4包含四个电阻器容差，因此有 16 个可能的误差因素。如果我们调查所有可能性，我们会发现误差范围从当所有电阻器容差都向同一方向变化时为零到 2T/（1–T）。

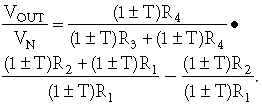
　　公式 4

　　当总容差为 1%（0.5% 电阻的 P+D）时，电阻容差可导致 CMR 的范围从高达运算放大器的限值到低至–34.89 dB。考虑到 1% 电阻器的采购和漂移容差，我们得到的 CMR 可低至 –24.17 dB。我们将此误差计算为 CMR 误差，但在没有共模电压和差分输入信号的情况下，它变成了增益误差。

　　分立差分放大器难以构建和微调，因此大多数设计人员都选择了内置微调电阻的 IC 差分放大器。低成本 IC 差分放大器提供高达 –86-dB CMR。

　　当我们分析我们的电路以确保长期性能和可制造性时，请记住无源元件具有购买和漂移容差，并且漂移容差可能大于购买容差。我们可以在制造过程结束时调整购买公差，但我们或我们的系统只能在进行测量之前调整漂移公差。非比率电路假设电阻容差的两倍，比率电路可以将误差降低到容差值。使用分立器件很难构建精确的差分放大器，但具有电阻微调和匹配能力的 IC 通常可以获得 –90 dB 的 CMR。

更多信息可以来这里获取==>>电子技术应用-AET<<