一种基于镜像原理修正传感器非线性误差的方法
摘要： 如何对传感器非线性误差进行修正是一个具有普遍意义的技术问题。基于镜像原理对传感器的非线性误差修正提出了一种软件方法，该方法克服了目前常用的诸如硬件补偿法、分段直线修正法、人工神经网络修正法等存在的弊端，同时用某霍尔式位移传感器的标定结果作为例子对该方法的具体应用进行了详细的论述。事实证明该方法操作简单，修正效率高，结果稳定可靠。
Abstract：
Key words :
一、引言
在测控系统中，一般采用传感器对被测参数进行拾取和转换。由于大多数传感器的输入/输出特性是非线性的，为了提高测量准确度，常需要对传感器的非线性误差进行修正，因此，如何对传感器非线性误差进行修正是一个具有普遍意义的技术问题。常用的方法有：
（1）硬件补偿法，该方法难以作到全程有效补偿，且存在补偿电路硬件漂移等问题；
（2）分段直线修正法，该方法存在不连续、不光滑，对所标定的某些点的依赖性大，极可能不过零点的弊端；
（3）人工神经网络修正法，这是近几年兴起的新方法。该方法具有使用的样本数少、算法较简单等优点，应用前景良好，但已经掌握该技术的人不特别多，使用推广受到一定程度的限制。
因此，在这里基于最小二乘法[1]并模拟镜像原理对传感器非线性误差的修正提出了一种新方法。
（1）硬件补偿法，该方法难以作到全程有效补偿，且存在补偿电路硬件漂移等问题；
（2）分段直线修正法，该方法存在不连续、不光滑，对所标定的某些点的依赖性大，极可能不过零点的弊端；
（3）人工神经网络修正法，这是近几年兴起的新方法。该方法具有使用的样本数少、算法较简单等优点，应用前景良好，但已经掌握该技术的人不特别多，使用推广受到一定程度的限制。
因此，在这里基于最小二乘法[1]并模拟镜像原理对传感器非线性误差的修正提出了一种新方法。
二、非线性误差修正的镜像原理
设P（i=，2，....n为P（Yi﹒Y（Y﹒Y不但连续，而且必过零点，甚至可以高阶光滑，这正是我们所期望的结果。）对输出Y有效地发挥着“兴小衰大”的动态调节作用，而修正曲线z=f(Y)。显然，镜像曲线y=f）相乘就得到了传感器的非线性误差修正曲线z=f(Y)点关于直线Y=X的一类特殊的镜像。显然，如果P点在直线Y=X上方偏离该直线越远，即其纵坐标越大，则镜像点Q在该直线下方偏离它也越远，即其纵坐标越小，反之亦然。如果将P点的纵坐标Yi与镜像点Q的纵坐标Xi/ Yi相乘，不难发现该乘积就成了输入值Xi。因此，将传感器的输出曲线即P点所在的曲线Y与其镜像曲线即镜像点Q所在的曲线y=f）为传感器标定时得到的一系列点，设点Q（Yi，Xi/Yi）1（Xi，Yi）
三、非线性误差修正方法
（1）设点P为传感器标定时得到的足够多个离散点，其中Xi0，i=，2，...
（2）采用描点法描出点 P关于直线Y=X，根据镜像点的分布情形设的镜像点Q（Yi，Xi/Yi）（Xi，Yi），n（下同）。1为标准输入，Yi为对应的输出值，且Yi≠（Xi，Yi）
（2）采用描点法描出点 P关于直线Y=X，根据镜像点的分布情形设的镜像点Q（Yi，Xi/Yi）（Xi，Yi），n（下同）。1为标准输入，Yi为对应的输出值，且Yi≠（Xi，Yi）
计镜像曲线y=f（Y
（3）用最小二乘法拟合曲线的原理求出y的待定系数即确定了镜像点Q所在的镜像曲线。
（4）将y与传感器输出Y。相乘即得到非线性误差修正曲线z(Y)=y(Y)Y(Y)(Yi，Xi/Yi)(Y)）的合适形式。在其定义域内，该曲线可以是多项式、指数函数、对数函数、幂函数等，甚至可以是它们的任意组合形式。（Y）
（3）用最小二乘法拟合曲线的原理求出y的待定系数即确定了镜像点Q所在的镜像曲线。
（4）将y与传感器输出Y。相乘即得到非线性误差修正曲线z(Y)=y(Y)Y(Y)(Yi，Xi/Yi)(Y)）的合适形式。在其定义域内，该曲线可以是多项式、指数函数、对数函数、幂函数等，甚至可以是它们的任意组合形式。（Y）
四、非线性误差修正实例
因任何一个初等函数均可以用一个适当的k/输出特性为准线性，且较难准确判断镜像点Q的镜像曲线y的合适形式时，其镜像曲线可设为一个标准的多项式，其次数k可根据需要人为或由计算机根据非线性误差限等自动确定，但应满足k≤n+1。
(Y)=f(Y)（Yi，Xi/Yi）次多项式去充分逼近它，当传感器的输入
(Y)=f(Y)（Yi，Xi/Yi）次多项式去充分逼近它，当传感器的输入
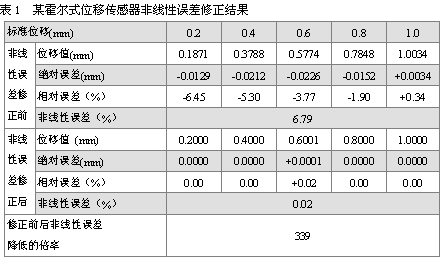
这里以表1中所示的某霍尔式位移传感器标定数据[2]/输出特性为准线性的，可设镜像点Q的镜像曲线为一个三次多项式，即：（Yi，Xi/ Yi）为例来说明非线性误差修正的具体方法。基于其输入
（1）
由表1数据，并根据上文所述非线性误差修正方法可得到标定点（0.2, 0.1871）、（0.4, 0.3788）、（0.6, 0.5774）、（0.8, 0.7848）、（1.0, 1.0034）对应的镜像点为（0.1871, 0.2/0.1871）、（ 0.3788， 0.4/0.3788）、（0.5774，0.6/0.5774）、（0.7848, 0.8/0.7848）、（1.0034，1.0/1.0034）。这些镜像点所在的镜像曲线的待定系数可根据第三条借助计算机求得，即：
aa´10-2;a´10-2 a´10-23=1.828396904320512=-6.150873642483691=-3.787355198643510=1.07808300655524
故所求得的镜像曲线为：
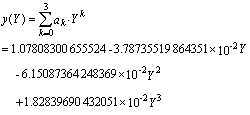2）（
故所求得的非线性误差修正曲线方程为：
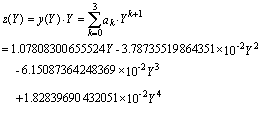3）（
参数Y代表Y(含所带的正负符号)的最大值与最小值之差。由表1知，采用本方法经软件修正后，传感器非线性误差由原来的6.79%降低到0.02%，即降低了近339倍，可见修正结果非常理想。的修正值。位移值的非线性误差等于在整个标定范围内其相对误差代表传感器的位移输出值，z(Y)
五、结束语
理论分析和事实表明，该修正方法原理简单，修正效率高，结果稳定可靠。不难看出，镜像曲线y的形式设计是否合理，是决定修正效果的关键因素，如果遇到修正后非线性误差不太理想的情况，则说明我们在上文所述非线性误差修正方法部分设计的镜像曲线的形式不太合理，即镜像曲线本身应该有“拐点”而我们在设计镜像曲线时却忽视了。
此内容为AET网站原创，未经授权禁止转载。