一种改进的中轴骨架三维模型检索算法
2008-07-03
作者:张学锋
摘 要: 针对三维模型" title="三维模型">三维模型检索算法性能较低的问题,提出了一种改进的中轴骨架三维模型检索" title="三维模型检索">三维模型检索算法。
关键词: 三维模型检索,特征变换,中轴骨架,骨架二叉树
随着激光扫描技术的发展以及计算机性能的提高,三维模型在很多应用领域中扮演着非常重要的角色,如工业产品的模型设计、虚拟现实系统、游戏设计、逆向工程以及仿真等,但是,要想构造一个真实感较强的模型其工作量巨大。目前在因特网和特定领域的数据库中存在着数以兆计的模型,且还在源源不断地增加。如果能够重复利用已有模型,就可大大减小模型设计的工作量。因此,对三维模型检索技术的研究已变得越来越紧迫和重要。
目前,三维模型检索主要采用基于内容的检索方法。根据特征提取方法的不同,可将检索方法大致分为四类:统计特征、函数投影、拓扑结构" title="拓扑结构">拓扑结构特征和基于几何结构分析。
基于统计特征的三维模型描述方法[1],不需要通过模型进行标准化处理,因此计算较为简单,具有良好的不变性。但是,这些特征描述模型之间相似性的能力普遍不够强,对三维模型本身内容的描述也不够充分。
基于函数投影的方法首先是将原始的三维模型投影至一个标准函数模型中[2],然后再计算特征向量。其优点在于其将三维模型投影为一系列不同视角的二维图像,从而大大减低了匹配的复杂度。但在函数投影过程中容易丢失一些重要的三维结构信息,因此检索的准确性不够理想。
基于模型拓扑结构特征的方法主要是根据模型的几何信息和拓扑结构获取模型的特征描述。Hilaga等人提出一种使用多分辨率Reeb图MRG(Multiresolution Reeb Graph)结构表示三维模型的方法[3]。而Sundar利用模型骨架描述三维模型的特征[4],该类方法能很好地描述模型本身的特征,可以获得较高的检索准确率,但该方法计算量较大。
基于几何结构分析的形状特征的方法由于能较好地描述模型的高层结构信息而受到广泛关注。Vranic等人[5]基于三维离散傅立叶变换的方法提取三维模型的特征。当三维模型可以被分割为一组规范化的特征集合并且特征之间的对应关系明确时,该方法具有很好的效果。然而,对于广义的三维多边形模型而言,实现上述条件是非常困难的。
因此,如何提高三维模型的检索性能,就成了十分突出的问题。本文提出一种基于整数中轴骨架的三维模型检索算法,该算法的关键思想是将三维模型的拓扑特征和统计特征相结合。首先,对待匹配的三维模型进行预处理;然后改进Hesselink提出的整数中轴算法[6],得到模型的中轴骨架,对骨架按区域划分,构造骨架二叉树" title="骨架二叉树">骨架二叉树,同时根据区域的大小定义节点的特征权值" title="权值">权值,用于衡量其对三维模型整体相似性的影响程度;最后,通过计算两个骨架二叉树的相似度,获得两个三维模型的相似度,在匹配过程中,采用由粗到细逐步淘汰的策略,不断缩减待匹配模型的范围,从而降低了模型匹配的时间。实验结果表明,该算法可以得到较好的检索性能。
1 模型预处理
对于同一种检索算法,处于不同坐标系下的三维模型应该具有相同的相似度。因此,检索算法在计算三维模型几何特征之前,应该对三维模型进行姿态调整,使其坐标系一致。
本文采用主元分析法PCA(Principal Component Analysis)对模型进行姿态调整[7]。该方法首先根据三维模型点集合的协方差矩阵计算出相应的特征值λ1>λ2>λ3,其对应的特征矢量为(I1,I2,I3),以(I1,I2,I3)为新的坐标系统,对三维模型进行坐标变换,得到变换后的坐标值。处理结果如图1所示。

2 骨架提取
设r是三维模型表面上的点,由Hesselink的整数中轴算法可得:
若e∈E,(E={e∈I3||e||=1}),I3为模型内部的一个体素网格点,则当m=r+1/2e时:
||m-ft(r+e)||=||m-ft(r)|| (1)
式中,m为整数中轴骨架上的一个骨架点,ft(r)为点r的特征变换函数。
为了记录以骨架点m为球心的内接球的半径,对整数中轴骨架进行改进,定义一元函数:
σm=||m-ft(r)|| (2)
式中,σm为骨架点m的权值。
由Hesselink整数中轴算法得到的骨架是一些比较散乱的骨架点,如图2所示。而一个好的中轴骨架应具有以下三个特性:相邻性、一致性和简洁性[2]。因此,本文对获得的骨架点进行以下优化。

如果q为三维模型表面上的一个网格点,B是一个网格点的集合,则可以在中轴骨架上找到一个点p,使得p=IMAS(q)(IMAS(q)表示对点q进行整数中轴骨架变换)。同样对于任意一个中轴骨架点p,对其进行整数中轴骨架变换的逆变换IMAS-1(p),就会得到一个与其相对应的三维模型表面网格点的集合。设q∈B,p=IMAS(q),点q和p之间的距离定义为dis(q)。定义一个辅助函数Average(dis(q)),其函数值为dis(q)(q∈IMAS-1(p))的平均值。所有的中轴骨架点应该满足:

将所有优化后的骨架点连接起来形成加权骨架H,如图3所示。

3 模型匹配
3.1 生成骨架二叉树
设δmax(ni)和δmin(ni)分别为骨架二叉树节点ni对应的中轴骨架区域Zi的Z轴坐标最大值和最小值。在进行更高一级细节层次划分时,按下面的公式计算每个区域的Z轴坐标最大值和最小值,骨架区域划分示意图如图4所示。


将区域Ci视为二叉树节点ai,其权值Wai为:

3.2 匹配骨架二叉树
设ai和bi(0≤i≤n)为三维模型P、Q对应的骨架二叉树中的节点,则它们的相似度函数为:
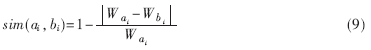
设三维模型P、Q的相似度函数为:

但是,在匹配过程中,由于模型的不同部分对模型整体的相似性的影响不同,因此对不同的sim(ai,bi)赋予不同的权值xi,对相似度函数加以改进,加入权值因子xi,改进的相似度函数为:
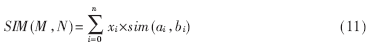
式中,![]() f(ai)为对应节点ai的区域大小,f(ao)为整个区域的大小。
f(ai)为对应节点ai的区域大小,f(ao)为整个区域的大小。
具体的匹配步骤如下:
(1)定义域值区间g=[0,β],β∈R;生成两个骨架二叉树的根节点ao、bo,若sim(ao,bo)∈g,则继续以下步骤;否则匹配结束,两个模型不相似。
(2)若ai、bi为非叶子节点,则生成ai、bi的左孩子节点a2i+1和b2i+1,若sim(a2i+1,b2i+1)∈g,则继续以下步骤;否则匹配结束,两个模型不相似。
(3)若ai、bi为叶子节点,sim(ai,bi)∈g,则该分支的匹配结束,向上回溯到其父亲节点,进行另一分支的匹配;若sim(ai,bi)∈g,则匹配结束,两个模型不相似。
(4)生成ai和bi的右孩子节点a2i+2和b2i+2,若sim(a2i+2,b2i+2)∈g,则继续以下步骤;否则匹配结束,两个模型不相似。
(5)若二叉树的任意节点ai和bi都满足:sim(ai,bi)∈g,(0≤i≤n),则两模型相似。
(6)重复执行(2)~(5)。
4 实验结果与分析
为了测试算法的效果,对本文方法、中轴骨架方法和形状分析方法的检索性能进行了实验和比较。实验在Windows平台上用VC++6.0语言实现,三维模型数据库采用普林斯顿大学形状分析小组提供的标准测试数据库[8],总共含有1 800个模型,采用典型的Precision-Recall曲线来度量不同方法的检索性能,三种方法的检索性能曲线如图5所示。由图可以看出,本文方法由于在拓扑结构的基础上融入了统计特征,因此在检索性能上有明显提高。

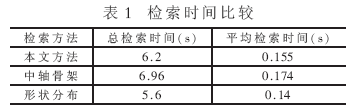
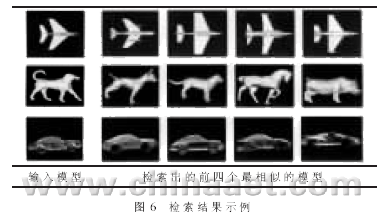
对于三维模型检索,另一个值得注意的问题是检索效率。如果检索时间过长,将导致实时性差,即使检索准确率有了明显的改进,其实用性也不强。本文采用改进的中轴骨架提取方法,它与传统的中轴骨架方法相比降低了算法的复杂度,但与形状分布方法相比在算法复杂度上有所增加,比形状分布方法需要更多的检索时间。但是,这种检索时间的差异很小,不会被用户察觉。对三种模型检索的具体实验验证环境是:CPU:Pentium 4 2.4GHz,内存512MB。对一批模型数据(40个模型)进行批处理,得到总检索时间和平均检索时间(检索时间包括打开文件读取模型数据的时间)如表1所示,检索结果示例如图6所示。
三维模型检索技术是近年来随着三维模型获取手段的增强、增多以及互联网的发展而兴起的计算机图形学领域内的一个重要课题。针对三维模型检索性能较低的问题,本文将三维模型的统计特征和拓扑特征相结合,提出了一种基于增强的中轴骨架三维模型检索算法。通过对本文方法的检索性能、检索时间进行测试,结果表明,该算法可以得到较好的检索性能。
参考文献
[1] TANGELDER J W H,VEHKAMP R C.Polyhedral model retrieval using weighted point sets.Journal of Image and Graphics,2003,3(1):209-229.
[2] 普建涛,刘一,辛谷雨,等.一种基于二维多边形集相似性的三维模型检索方法[J].中国图像图形学报,2004,9(12):1437-1442.
[3] HILAGA M,SHINAGAWA Y,KOHMURA T,et a1.Topology matching for fully automatic similarity estimation of 3d shapes proceedings of ACM SIGGRAPH.Los Angeles,USA,2001:203-212.
[4] SUNDAR H,SILVER D,GAGVANI N,et al.Skeleton based shape matching and retrieval proceedings of international conference on shape modeling and applications.Seoul,Korea,2003:207-216.
[5] VRANIC D,SAUPE D.3d shape descriptor based on 3d Fourier transform proceedings of IEEE EURASIP conference on digital signal processing for multimedia communications and services.Budapest, Hungary,2001:271-274.
[6] HESSELLINK W H,VISSER M,ROERDINK J B T M.Euclidean skeletons of 3D data sets in linear time by the integer medial axis transform[A].ISMM′2005[C].Paris,France,2005:259~268.
[7] VRANIC D,AAUPE D.3D shape descriptor based on 3D fourier transform[A].EURASIP conference on digital signal processing for multimedia communications and services[C].Budapest,Hungary:EURASIP,2001:271~274.
[8] SHILANE P,MICHAEL K,PATRICK M,et al.The princeton shape benchmark.In:Proc of the intern ational conference on shape modeling.Genova,Italy,2004:167-178.

