峰值电流控制模式有源箝位正激变换器的小信号模型与设计
2008-07-15
作者:李 华, 王志强
摘 要: 电流控制" title="电流控制">电流控制模式的补偿网络比电压控制模式的补偿网络容易调整,但是前者的建模要比后者的建模复杂得多。采用状态空间平均法为峰值电流控制有源箝位正激变换器" title="变换器">变换器建立了小信号模型,分析了箝位电路对变换器动态性能的影响,并给出了补偿网络的设计方法。
关键词: 峰值电流 小信号 建模 有源箝位正激变换器
在低压输出(3.3V或更低)场合,常采用同步整流的有源箝位正激变换器" title="有源箝位正激变换器">有源箝位正激变换器。但是,对其工作于峰值电流控制模式的动态分析却很少。
当采用峰值电流控制模式时,大多采样开关管" title="开关管">开关管电流进行控制,而这样就增加了控制难度,因为这时采样的电流不仅包括输出电感电流还包括励磁" title="励磁">励磁电感电流。由于箝位电路的存在,使得有源箝位正激变换器峰值电流控制模式的模型与正激变换器峰值电流控制模式的模型有很大区别。因此,本文介绍前者的小信号模型与设计,并给出其补偿网络。
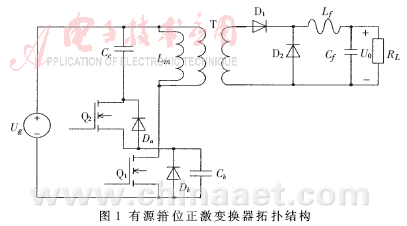
1 有源箝位正激变换器工作过程
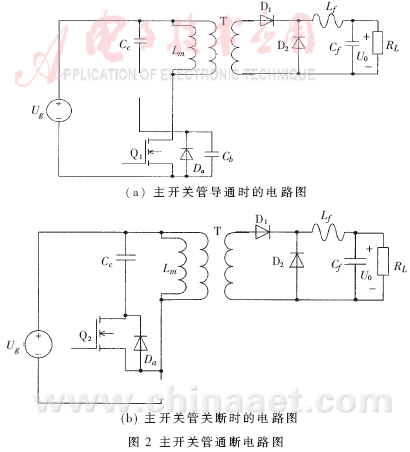
有源箝位正激变换器如图1所示。当开关管Q1开通时,电源电压施加于变压器初级绕组,同时接于次级绕组的D1导通,为负载提供能量,这段时间的电路为正激变换器,如图2(a)所示;当开关管Q1关断时,励磁电感给箝位电容充电,直到电容电压达到最大值,然后电容放电,同时接于次级绕组的D2导通续流。这段时间的变换器可等效为buck-boost变换器,如图2(b)所示[1-2]。所以,有源箝位正激变换器可以等效为两个电路:占空比为D的正激变换器和占空比为D的buck-boost变换器。两个变换器有共同的输入电压。
2 峰值电流控制模型
较常用的建模方法是状态空间平均法(state-space average)[3]。其他建模方法如开关网络、开关元件、等效受控源等方法都属于电路平均法的范畴[4]。峰值电流控制模式建模思路为:把功率级同电流控制环看成一个新功率级[5],该功率级的输入是给定电流ic,输出是电压Uo。模型建立后,即可为其设计补偿网络。
假定变换器工作在连续导通模式,并忽略转换过程,分别列出开关管开通和关断时输出电感和励磁电感的电压方程及输出电容和箝位电容上的电流方程。
在开关管导通阶段:
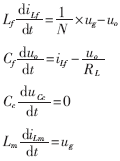
在开关管关断阶段:
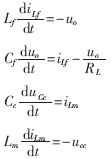
在整个开关周期求平均:
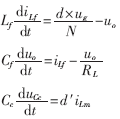
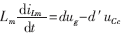
分离变量得直流工作点:
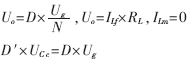
(式中,D是占空比,D′=1-Do)
线性化之后可得交流关系式:
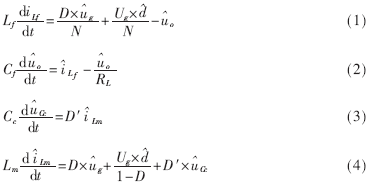
式中,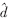 为占空比的扰动。
为占空比的扰动。
根据上面4个方程可为变换器建立小信号模型。首先根据式(1)和式(2)建立等效正激变换器模型,如图3(a)所示。然后根据式(3)和式(4)为等效buck-boost变换器建立模型,注意这里buck-boost变换器空载。也可以根据参考文献[4]与参考文献[6]直接建立buck-boost变换器的模型,如图3(b)所示。
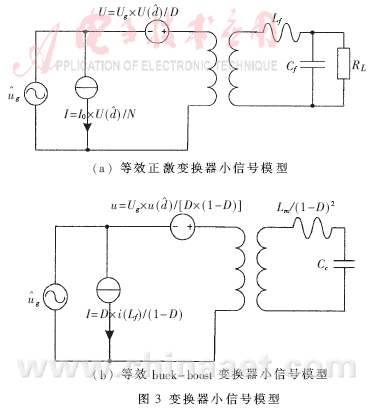
为变换器建立峰值控制模式的模型需要求等效功率级的传递函数,该传递函数为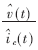 ,其中
,其中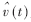 为输出电压的扰动,
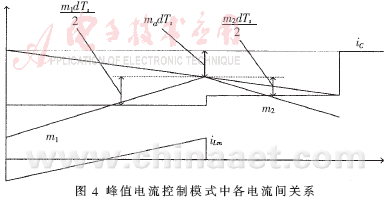
为输出电压的扰动,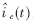 为给定电流的扰动。峰值电流控制模式中各电流间关系如图4所示[7]。由于采样的是开关管电流,所以该电流包括输出电感电流和励磁电感电流。为使变换器工作稳定,必须满足:
为给定电流的扰动。峰值电流控制模式中各电流间关系如图4所示[7]。由于采样的是开关管电流,所以该电流包括输出电感电流和励磁电感电流。为使变换器工作稳定,必须满足:
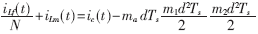
式中,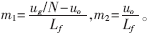 两者均为平均模型,分离变量后可得斜率的微变量为:
两者均为平均模型,分离变量后可得斜率的微变量为: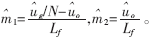 由于ma来自于芯片内部电压,所以可认为其恒定为Ma。一般取
由于ma来自于芯片内部电压,所以可认为其恒定为Ma。一般取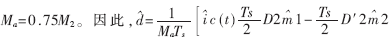
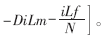 所以,可以用图5表示。图中:
所以,可以用图5表示。图中:
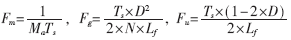
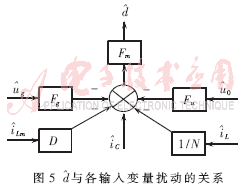
综合图3和图5,可得到有源箝位正激变换器的小信号模型,如图6所示。
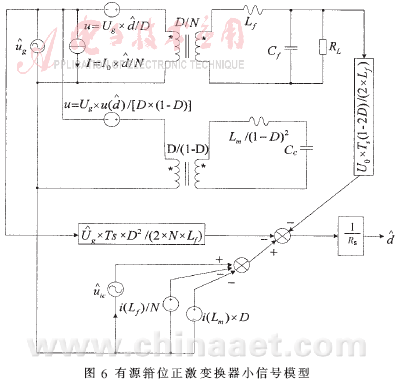
3 仿真分析
采用上述方法对一峰值电流控制模式有源箝位正激变换器进行建模分析。其相关参数为:输入电压48V,输出电压3.3V,输出功率50W,开关频率100kHz,励磁电感200μH,箝位电容120nF。采用图6的模型,进行仿真分析,其波特图如图7所示。
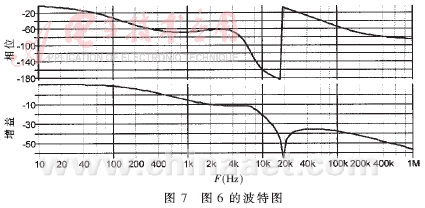
从图中可以发现,在大约20kHz左右有一个很严重的相位滞后,这是由于箝位电路影响而产生的。改变励磁电感和箝位电容的大小就可以改变滞后相位的大小。图8是箝位电容由100nF变化到1000nF的滞后相位的变化情况。从图8中可以发现,箝位电容越大,滞后相位越小。这是因为改变箝位电容大小,实际上改变了buck-boost变换器中励磁电感和箝位电容的谐振频率,从而影响滞后相位。当然箝位电容也不能选取太大[1],否则影响变换器性能。改进方法是:在箝位电容上串联一个电阻,可以改善滞后相位[7]。图9是没有串联电阻、串联10Ω和100Ω电阻传递函数的相位波特图。可见,串联电阻可以明显地降低相位滞后,这是因为串联电阻改变了箝位电路的品质因数Qc。
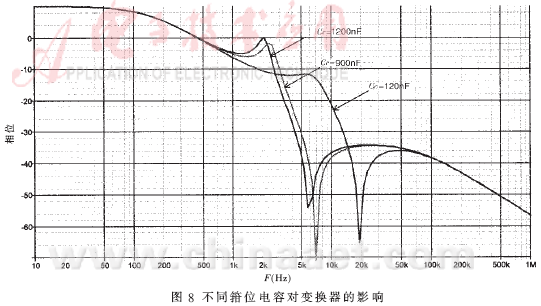
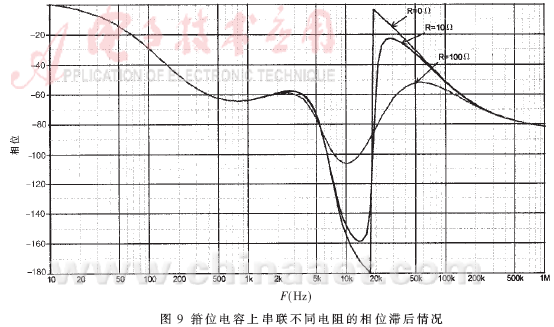
4 补偿设计
由图7的波特图可计算出其零极点,分别是fp1=-898Hz,fp2、3=-46.9±j10.4kHz, fp4=192.8kHz,fz1=-16.7kHz, fz2=90kHz,fz3=-156kHz。若改变励磁电感和箝位电容,则第一个极点和第一个零点都没有变化,而其他的零极点都有变化,这就是箝位电路对变换器的影响。图10为随Lm×Cc变化波特图的变化情况。可见,当Lm×Cc变大时,箝位电路部分由双重极点型变化为双极点型,且fp4变小而不能再忽略。根据上面分析,有源箝位正激变换器输出对给定电流的传递函数有三种:
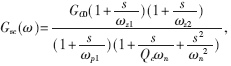
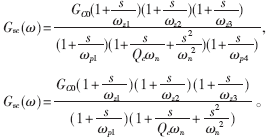
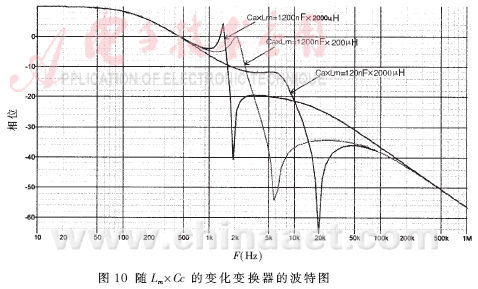
从零极点个数来看,可把前两个看成同样的类型,因为它们的极点数都比零点数多一个,而最后一个是另一类型,因为它的极点数等于零点数。这就决定了它们补偿方法的不同。对于前两种类型,可以采用单极点-单零点补偿网络,如图11(a)所示。对于后一种类型,可采用双极点补偿网络,如图11(b)所示。
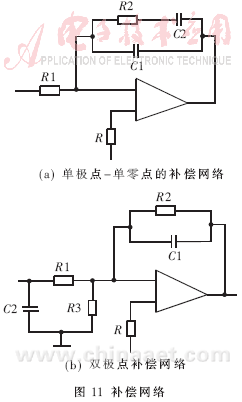
对于本文所举的例子,显然第一种补偿方法较为合适(可忽略大于开关频率的零点和极点)。采用图11(a)所示的单极点-单零点补偿网络,各参数为R1=58kΩ,R2=10kΩ,C1=18nF,C2=1nF。
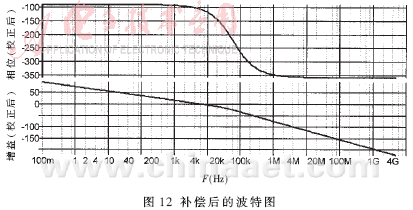
补偿后系统开环传递函数的波特图如图12所示。可见,补偿后,系统的带宽为3.6kHz相位裕量大约为60度。所以可满足系统稳定的要求。
参考文献
[1] 阮新波,严仰光.直流开关电源的软开关技术. 北京:科学出版社,2000.
[2] 张卫平.绿色电源; 现代电能变换技术及应用. 北京:科学出版社, 2001.
[3] MIDDLEBROOK R D, CUK S. A general approach to modeling switching-converter power stages. Power Electronics Specialists Conference, 1976.
[4] 胡炎申, 谢运祥.通信用高频开关电源技术发展综述.电源世界,2006,(3).
[5] 张卫平.开关变换器的建模与控制.北京:中国电力出版社,2006.
[6] Understanding buck-boost powerstages in Switchmodel Power Supplies.Unitrode Application Note. Unitrode Handbook,1999.
[7] FONTAN A, OLLERO S, CRUZ E, et al. Peak current model control applied to the forward converter with active clamp. IEEE APEC’98:45-51.

