摘 要： 介绍混合智能系统，并充分利用该系统在学习、自动模式识别和近似推理方面的优势,采用模糊神经混合方法对石油测井中的储层进行识别。该方法通过对测井数据的学习，运用模糊逻辑" title="模糊逻辑">模糊逻辑与神经网络相结合的混合系统对测井数据进行提取和优化;根据来自不同油井的观测数据，采用一个两阶段的策略决定预测模型的结构和参数,进而对测井储层进行识别。给出了该混合方法预测的初步结果，为油井的开发提供了重要的参考。
    关键词： 智能系统  模糊神经  储层识别  神经网络  模糊逻辑

    近年来采用模糊模型解决复杂的非线性问题的应用变得越来越广泛。本文提出一种能够对复杂的储层进行识别的模糊神经混合方法，并为测井岩性识别提供一种新的有效手段。其特点是不需要建立统计模式识别模型或岩性识别库，可通过对少量已知样本的学习建立测井信息和不同岩性之间的对应关系，并借助网络的推理联动功能实现对未知岩性的预测。
    依据测井数据建立一个模糊神经混合系统需要两个阶段。首先，为了建立模糊推理模型的结构和初始化参数，涉及一个竞争学习过程。与多数已存在的模糊神经方法相比，适当的模糊规则" title="模糊规则">模糊规则、隶属度函数数量和规则参数的初始值，在最初的学习阶段被决定；在第二个学习阶段，通过梯度下降法优化模糊规则的参数，一旦学习完成，这种网络结构就能使通过模糊规则形式获得的知识更加严密，并能按照模糊推理规则处理数据^[1]。
1 混合智能系统
    混合智能系统是指在不精确和不确定的环境中综合使用多种智能算法构成一个智能系统。智能系统的三个主要元素是模糊逻辑、神经网络和进化计算。其中，模糊逻辑主要进行非精确性处理和近似推理，神经网络使系统获得学习和适应的能力，而进化计算则广为采用遗传算法，提供随机搜索和优化的能力。图1所示为混合智能系统的几种方式。

                           
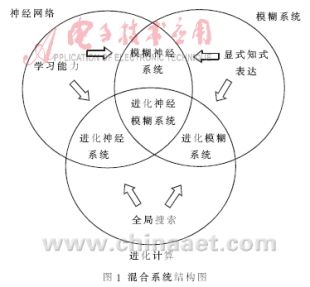
    在模糊神经混合方式中，实现智能系统的关键是：(1) 如何利用模糊系统" title="模糊系统">模糊系统原理修正神经网络的参数及结构（称为模糊-神经系统）。(2) 如何利用神经计算方法来调节模糊逻辑系统的行为（称为神经-模糊系统）。
    本文主要讨论模糊神经网络，就是将模糊逻辑系统同神经网络有机地结合起来。神经网络在学习和自动模式识别方面有极强的优势，采用神经网络技术进行模糊信息的处理，可以使模糊规则的自动提取和模糊隶属函数的自动生成得以解决，从而使模糊系统成为自适应的模糊系统。将具有逻辑推理能力和高阶信息处理能力的模糊技术引入神经网络，可以大大拓宽神经网络处理信息的范围和能力，使其不仅能处理精确信息，也能处理模糊信息。模糊神经网络汇集了神经网络与模糊理论的优点，使整个系统具有较强的学习能力和表达能力。
2 模糊神经混合系统
    为了提高模糊神经混合系统的精确性和可解释性，该系统主要由三个部分来实现：(1)根据模糊规则从训练数据中提取信息。(2)为了提高系统的精确性，精简模糊规则。(3)通过一个优化过程，增加模糊规则的可解释性。
2.1系统结构
    岩性识别模型是基于模糊系统与神经网络构建而成的。基本的模糊系统结构与Takagi-Sugeno模糊结构相似。Takagi-Sugeno模糊模型是由Takagi、Sugeno和Kang（简称TS）构成的^[2]，这个模型是从给定的输入-输出数据集中产生模糊规则，以此形成系统的方法。TS模糊推理系统规则如下：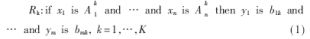

式中，x_i(i=1,…,n)是输入变量，y_j(j=1,…,m)是输出变量，A_i^k是定义在输入变量上的模糊集，b_jk是定义在输出变量上的模糊单体，A_i^k是通过高斯隶属函数来定义：
   
式中， c_ik、δ_ik为高斯函数的中心和宽度，通过采取单模糊化、乘法规则推理以及中心平均法去模糊化，对于任意输入向量X，推理的确切输出为：
   
式中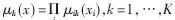，,为第k个规则的激活强度。
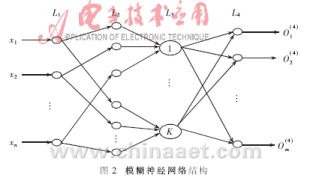
    为了清楚地了解前面提到的模糊推理机制，为此提出一种神经网络，其结构如图2所示，由如下四层构成^[3]：
    (1) 第一层有n个输入节点x_i(i=1,…,n)。
    (2) 第二层由k组节点构成，每一组又有n个单元，通过这些节点可以估计出高斯隶属函数的值。
    (3) 第三层由k个单元（与k个模糊规则有关）构成。每一个节点计算出一个规则的权值" title="权值">权值。
    (4) 依据(3)的结果，第四层提供最终的输出。

                           
2.2 学习策略
    模糊神经混合系统的学习策略主要由两个阶段组成。在第一阶段，规则节点的值、网络的结构、规则参数的初始值（权值）通过竞争学习策略获得；在第二阶段，通过有导师学习的策略，调整所有的参数。为了实现这一学习策略，必须提供一个由输入输出数据构成的训练集和一个初始假定的模糊规则值K。
    在竞争学习阶段，主要是如何决定规则节点的值和初始权值。对模糊模型来说，根据规则的数量，一个输入空间聚类" title="聚类">聚类自动提供适当的聚类数量，这并不像通常的基于聚类的方法，如：C-均值、模糊C-均值、聚类的数量、规则的数量都必须事先选定。竞争学习阶段仅涉及模糊神经网络的第三层，当一个输入向量被加载进来时，这一层的节点进行竞争，根据输入向量的欧氏（即欧几里得）距离的大小^[4]，它们中的一个被选中作为最优获胜者，同时将第二个距离输入向量最接近的点作为次优获胜者。为了使最优获胜者和次优获胜者更加接近，并分别使它们远离输入向量，必须更新它们的权值向量。这一竞争－惩罚机制是假定每一个聚类仅仅通过一个权值向量被表现出来。
    初始化后，从向量中提取模糊规则。例如建立网络的结构和初始化权值。在第二个学习阶段，根据同样的训练数据优化、调整参数，最终提高整个系统性能^[5]。有导师学习的算法是依据梯度下降的方法，在一个网络权值空间上实现。
3 在岩性预测中的应用
    在岩性预测领域，充分利用模糊系统与神经网络相结合的优势，通过对相关测井数据参数的提取和优化，主要选取与岩性关系密切的测井数据，例如自然伽玛（GR）、自然电位（SP）、声波时差（AC）、密度（DEN）、补偿中子（CNL）、电阻率（RT）、深侧向电阻率（RD）、浅侧向电阻率（RS）等，充分应用已有的岩性判别规则：GR和SP作为泥质指示器，是划分泥岩及高放射性岩性的重要参数；RT反映了不同岩性的电性差异；AC、DEN、CNL与岩性也有重要关系等。通过对这些重要参数的预测，可以基本确定该地区油井的岩石成分，从而为油井的有效开采提供重要的参考价值。
    从已经获得的测井数据中预测岩石成分是主要的工作，但是这种非线性预测也是非常复杂的。为了作出准确的预测，必须考虑多种因素。而且不同的地区，它们的地质构造也有很大差别，常常会遇到一些常规技术难以解决的问题。例如，岩石成分复杂多样，泥质含量在含砂层无法求得等。
    本文通过分析甘肃泾川地区的测井资料，发现该地区的岩石成分主要为泥岩、砂岩、钙质、煤层、长石、页岩六种。采用与岩石成分关系密切的五种输入数据：SP、GR、AC、RT、CNL作为输入参数，一共采用45组试验数据进行预测分析，其中每一组数据由5个向量构成，前32组数据用作训练数据，后13组数据用于对训练结果进行测试。由于这些变量的取值范围不同，需要对变量进行预处理。为了使所有的数据在一个固定范围内变化，基于每一个变量的均值和方差，通过一个再次缩放过程^[6]，最终使数据的格式规一化。
    模拟过程分为两个阶段：模糊神经系统的学习和系统性能的计算。预处理数据被分成训练数据和测试数据。通过模糊神经系统两个阶段的学习策略，训练数据用来建立模糊模型，测试数据则用来检查模糊模型的预测能力。
    通过设定不同的学习参数，运行竞争学习算法便可得到不同的模糊模型。首先，假定采用十个规则作为先验知识(因模糊神经系统的初始化结构基于这些规则),
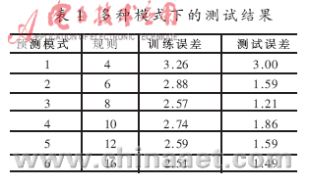
    因此，开始的模糊神经网络有32个输入，6个输出，10个规则节点。第二个学习阶段，运行1000次，依据测试数据估计最终模糊数据的预测精度。运行结果如表1所示，对每一个产生的模糊推理模型来说，训练和测试数据的均方误差以及模糊规则的数量被显示出来。由表1可以看出，对训练和测试模型来说，推理模型分别提供了比较好的预测结果，而且，如果规则选择恰当，误差就会变小。对于非常复杂的预测和初始变量具有很大不确定性的问题，效果尤其显著。

                   
    最初规则数增加，误差下降。但随着规则数的继续增加，误差又逐渐变大。这表明随着问题复杂性的增加，精确性有所下降，这也与实际情况相吻合。对于一个特殊的测试模式来说，图3比较了一个测试模式预测的所有输出值。从中可以看出，该模式的预测值与实际值就非常接近了。

                        
    在储层识别中采用模糊神经混合方法，不仅快速、有效，而且初步的试验结果表明，尽管该预测问题复杂且数据量有限，但模糊模式结构简单，预测的精度基本令人满意。在以后的研究工作中，将重点考虑如何进一步获得更高的精度以及这种提取模型的可解释性。为了实现这一目标，适当选取更多的输入变量，不仅可以提高预测的精度，而且也能够提高模糊模型的可解释性。
参考文献
[1] CASTELLANO G, CASTIELLO C. A neuro-fuzzy system for Ash property prediction. Second international workshop on Intelligent systems design and application. table of contents. Atlanta Georgia,2002:175-180.
[2] SUGENO M, KANG G T. Structure identification of fuzzy model. Fuzzy Sets and Systems,1988,(28):15-33.
[3] CASTELLANO G, CASTELLANO C, MARIA A. KERNEL:A matlab toolbox for knowledge extraction and refinement
 by neural learning. ICCS, 2002.
[4] 吴晓莉，林哲辉.MATLAB辅助模糊系统设计[M]. 西安:西安电子科技大学出版社，2002.
[5] 楼顺天，胡昌华，张伟.基于MATLAB的系统分析与设计-模糊系统[M]. 西安:西安电子科技大学出版社，
 2003.
[6] BISHOP C M. Neural network for pattern recognition.Oxford: Clarendon Press, 1995.