对被噪声污染的正弦波信号进行频率估计是信号参数估计中的经典问题,目前国内外已提出不少方法。文献给出了在高斯白噪声中对正弦波信号频率进行最大似然估计算法,该算法能够达到卡拉美-罗限(CRB),但计算量大,实现困难。FFT频率估计方法具有速度快、便于实时处理的特性而得到了广泛应用。但FFT频率估计方法得到的是离散频率值,当信号频率与FFT离散频率不重合时,由于FFT的“栅栏”效应,信号的实际频率应位于两条谱线之间。显然仅仅利用FFT幅度最大值估计信号频率难以满足精度要求,因此各种插值算法应运而生。文献给出了Rife算法,在对输入信号进行一次FFT运算后,利用最大谱线及其相邻的一根次大谱线进行插值来确定真实频率位置。当信号的真实频率处于两相邻量化频率之间的中心区域时,Rife算法精度很高,但是在FFT量化频率附近的误差却较大。文献提出了一种修正Rife算法,通过对信号进行频移,使新信号的频率位于两个相邻量化频率点的中心区域,然后再利用Rife算法进行频率估计。文献提出了基于傅里叶系数插值迭代的频率估计方法,该方法能够有效提高精度,但需要多次串行迭代,不利于发挥FPGA并行处理的优势。本文分析了以上3种算法的特点,并以之为基础结合FPGA的并行处理优势,提出了一种利用信号FFT插值系数的幅度和相位信息来构造频率修正项的新算法。
1 基于FFT插值的正弦波频率估计法
1.1 算法原理
单一频率正弦信号表示为:
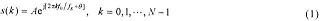
式中:A,f0,θ分别为正弦信号的幅度、频率和初相;fs为采样频率。目前基于FFT的正弦信号频率估计分为2个过程来实现:粗测频和精测频。粗测频通过直接观察FFT幅谱最大值点m来完成,受观测时长T的限制,误差范围为±l/(2T)。假设为信号频率的真实值,δ为信号频率与其FFT幅度最大处对应频率的相对偏差,m,与δ的关系如式(2)所示:

考虑到FPGA并行计算的特点,利用流水线结构同时计算多个Xm+p,Xm+p-1值,将串行迭代变为并行迭代,其运算步骤归纳如下:

本文提出的算法分为粗测频(步骤1)和精测频(步骤2,3),频率估计值为粗测结果与精测结果之和。
1.2 算法分析
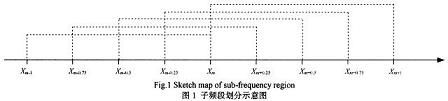
本文算法与文献提到的算法主要区别在于步骤3。算法将正弦波信号所在频段[m-1,m+1]细化为5个子频段,如图1所示,并根据δ1值的大小判断信号谱线位置,使信号的频率位于某子频段的中心区域再进行频率估计。
该算法也可认为是对Rife算法的一种修正,通过适当增加运算量提高了估计精度。当p=O及p=1时,该算法退化为Rife算法。
与MRife算法相比:MRife算法是通过对原始信号进行平移,然后对平移后的信号做FFT,重新用Rife算法计算δ。从式(3)可以发现“信号平移+FFT”与Xm+p时域运算是一致的,所不同的是,由于计算单个Xm+p只需N次复数乘法和N次复数加法,运算量比“信号平移+FFT”小,因此本文算法可同时计算多个Xm+p,Xm+p-1,以提高估计精度。
2 算法硬件实现
本文算法充分利用了FPGA并行计算的优点,在FPGA实现时采用流水线模式,经过固有时间后,每个时钟周期可以输出一个指定操作的结果,提高了算法的运算速度。
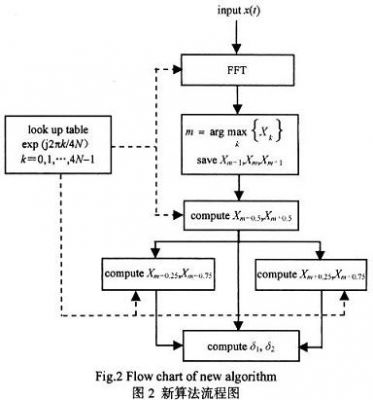
从前面的分析可知,整个测频算法主要包括粗测频和精测频2个部分:首先对信号作FFT运算并进行谱峰搜索得到峰值位置;再通过插值FFT运算得到频率偏差δ1,δ2;粗测频部分可以直接调用相关FPGA的FFT库函数完成。从式(3)可知精测频部分需要大量计算三角函数,本文采用查表法来实现。整个算法流程如图2所示。
3 仿真分析
信噪比定义为: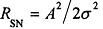 ,σ为噪声均方误差。对正弦波信号,在相位、幅度和频率3个参数均是未知的情况下,频率估计的方差下限为:
,σ为噪声均方误差。对正弦波信号,在相位、幅度和频率3个参数均是未知的情况下,频率估计的方差下限为:
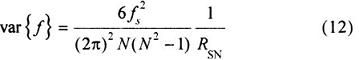
式中N为样本数。在仿真中设fs=167 MHz,N=512,因此两条谱线间的频率差为△f=fs/N。现取fi=45.5△f+(i-1)△f/20(i=l,2,…,21)的正弦波,即对应FFT后峰值位置与信号真实峰值偏差δ为[-0.5,0.5]。对每个频率fi的取值分别作l 000次Monte Carlo试验,计算δl,δ2的均方根误差(RMSE),定义比率R=RMSE/CRB,仿真结果如图3、图4所示。RSN取-20 dB~0 dB,步长为0.5 dB,分别做1 000次Monte Carlo试验,计算新算法的归一化频率估计均方误差,仿真结果如图5所示。
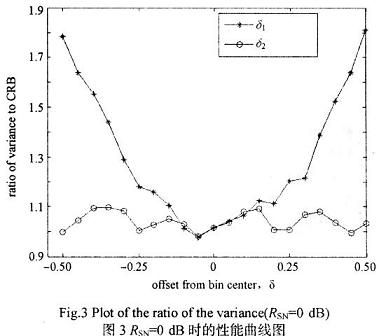
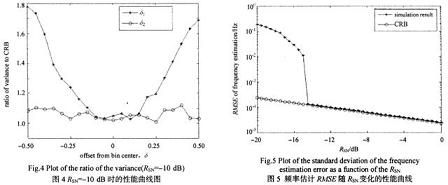
仿真结果表明δ2不随被估计信号的频率分布而产生波动;当RSN>-14 dB时,新算法频率估计值的方差在整个频段都接近卡拉美-罗限,具有稳定的性能。
4 结论
本文在分析Rife,MRife和傅里叶系数插值迭代3种算法的基础上,将串行迭代变为并行迭代,由此得出了一种快速频率估计算法,并分析了新算法与前3种算法的异同。计算机仿真结果证实新算法能够快速、高精度估计单频信号的频率,便于工程实现,适合应用在雷达、电子对抗等对处理实时性要求非常高的领域。

