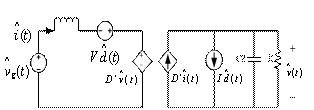0 引言
传统单相升压APFC电路已经被广泛应用到功率因数校正电路中,但是该方案需要独立的不可控整流桥,置后的升压电感需要解决抗直流偏磁问题,而且升压电感的位置很不利于整个功率电路的集成。这些引起了人们对传统单相升压APFC电路的重新思考,设想在利用其成熟控制思想与现成控制电路的前提下,使整个功率电路便于功率集成。近年来在这方面已经取得了很大进步,有多种电路拓扑被提出,其中双向开关前置的单相升压APFC变换器电路凭借其特有的性能引起了人们的关注。
1 双向开关前置的单相升压APFC变换器电路结构
双向开关前置的单相升压APFC变换器的电路如图1所示。输入部分有交流电压源VS和滤波电容C1组成。双向开关S1和电感L完成功率因数校正功能,其中双向开关S1由D5、D6、D7、D8和V1组成。整流部分由D1、D2、D3、D4构成,C2起储能和输出滤波的作用,R为负载。
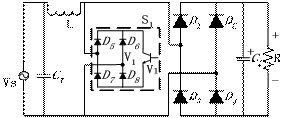
图1 双向开关前置的单相升压APFC变换器主电路
2 双向开关前置的单相升压APFC变换器电路工作状态分析
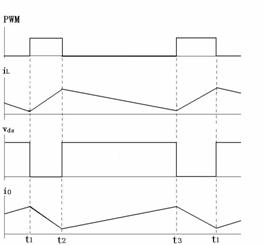
下文将对双向开关前置的单相升压APFC变换器电路动作过程进行分析。在连续导通模式下,对应开关管的一个高频周期,流过电感L的电流iL,加在开关管V1两端的电压Vds和输出电流i0的波形如图2所示。对应各段时间的等效电路如图3所示。其中工作状态1和工作状态2是工频正半周时的情况,工作状态3和工作状态4是工频负半周时的情况,后两个状态只是前两个状态在负半周的重复。为了分析方便,各二极管和开关管的导通压降看作零,等效电路中的D1、D2、D3、D4、D5、D6、D7、D8仅表示电流流过的通路,C2看作足够大,保证输出电压恒定,C2很小可以忽略不计。
(a)正半周一个周期的波形

(b)负半周一个周期波形
图2 变换器电路开关动作时iL、Vds、i0的波形
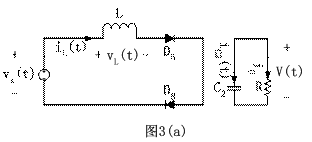
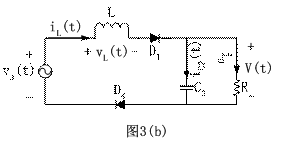

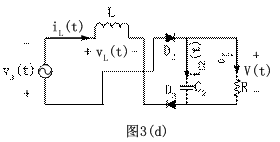
图 3 各种工作状态时的等效电路
2.1当VS处于正半周时的工作状态
工作状态1(t1
工作状态2(t2
2.2当VS处于负半周时的工作状态
工作状态3(t4
工作状态4(t5
3 双向开关前置的单相升压APFC变换器电路小信号建模
对于双向开关前置的单相升压APFC变换器电路而言,在CCM工作模式下,由于后两个状态只是前两个状态在负半周的重复,下面以正半周期两个状态为例进行分析。为了求解变换器的静态工作点,需要消除变换器中各变量的高频开关分量,通常采用求平均值的方法。在满足低频假设和小纹波假设的情况下,定义变量电感电流i(t)、电容电压v(t)和输入电压vs(t)在开关周期Ts内的平均值
为了简化分析,将有源开关元件与二极管都视为理想元件。则在CCM模式下变换器的每个开关周期都有两种工作状态。可以分别列出电感电压和电容电流的微分方程式(1)、(2)、(3)、 (4),然后结合(5)、(6)、(7)式就可以分别得到电感电压和电容电流在一个开关周期内的平均值,进一步可以导出变换器的一组非线性平均变量状态方程(8)、(9)。
(8)、(9)是一组非线性状态方程,各平均变量和控制变量d(t)中同时包含着直流分量和低频小信号分量。在电路满足小信号假设的情况下,可以分离出电感和电容的交流小信号状态方程为(10)、(11)。
变换器的实际工作状态是工作在静态工作点附近并且按线性规律变化。但是(10)、(11)两式组成的交流小信号状态方程仍为非线性状态方程,因此还需要对非线性方程线性化。由于(10)、(11) 两式中除了
根据方程 (12)、(13)可以建立更为直观的交流小信号等效电路模型,为分析变换器的小信号特性提供方便,如图5所示:
图4 双向开关前置的单相升压APFC变换器在CCD模式下的交流小信号等效模型
4 双向开关前置的单相升压APFC变换器仿真分析
下面利用Matlab7.1中的Simulink6.0仿真软件对变换器电路进行仿真,假定参数设置如下:Vs=220V,初级电感L=1×10-3H,初级滤波电容C1=3.3μF,输出储能电容C2=200~5000μF,开关管的工作频率为fS=50KHz,负载R=20~140Ω。下面分别讨论储能电容C2和负载R的变化对功率因数(PF)和输出纹波电压(Vpp)的影响。
4.1参数变化对电路的功率因数(PF)的影响
参数变化会对电路的功率因数(PF)产生影响,以桥臂并联电容C2和负载R为变量,仿真求得电路的PF值,结果如表 1所示:
表 1 功率因数随输出侧并联电容值及负载变化的仿真结果
功率因数
(PF)
负 载 电 阻R(Ω)
20
40
60
80
100
120
140
C2
(uF)
500
0.950
0.954
0.952
0.951
0.949
0.945
0.941
1000
0.949
0.953
0.951
0.949
0.948
0.943
0.938
1500
0.949
0.952
0.953
0.952
0.948
0.936
0.924
2000
0.951
0.954
0.955
0.950
0.942
0.921
0.886
2500
0.950
0.955
0.954
0.942
0.935
0.908
0.875
电容C2分别取500uF、1000uF、1500uF、2000uF、2500uF时,负载在20Ω~140Ω范围内对应分别取7组数据,利用MATLAB软件对各PF值进行三次多项式插值,插值后的变化曲线如图5所示。
图5 功率因数随输出侧并联电容值及负载变化的PF插值曲线
从图5可以看出,针对某一取值的电容,负载的变化对功率因数有很大影响,当40Ω≤R≤60Ω时,功率因数取得较大值。
4.2参数变化对电路的输出纹波电压(Vpp)的影响
参数的变化同样会影响电路的输出纹波电压(Vpp),以桥臂并联电容C2和负载R为变量,仿真求得电路的输出纹波电压值如表2所示。
表2 输出纹波电压随输出侧并联电容值及负载变化的仿真结果
输出纹波电压
Vpp(V)
负 载 电 阻R(Ω)
20
40
60
80
100
120
140
C2
(uF)
500
120
84
59
46
39
33
30
1000
83
42
31
23
18
14
12
1500
60
30
18
15
12
10
7
2000
42
21
15
12
10
8
6
2500
30
17
12
10
8
7
5
电容C2分别取500uF、1000uF、1500uF、2000uF、2500uF时,负载在20Ω~140Ω范围内对应分别取7组数据,利用MATLAB软件对输出纹波电压(Vpp)进行三次多项式插值,插值后的变化曲线如图6所示。
图6 功率因数随输出侧并联电容值及负载变化的PF插值曲线
从图6可以看出,纹波电压值随负载电阻的增大而减小,负载电阻越大,纹波越小,输出电压越平滑。在实际应用中要同时兼顾设计要求和成本,一般来讲输出电压纹波(Vpp)在满载的情况下不大于20V就可以满足要求,这时候要尽可能考虑到成本,电容体积等因素,所以C2取1500uF左右即可。
综上所述,如果要求输出纹波电压VPP在20V以内,电容又不太大,优先考虑功率因数的情况下,结合体积、经济性等因素,则该电路的最佳参数选择为:C2取值在1500uF左右,R取40Ω≤R≤60Ω。
4.3最佳参数情况的实例仿真
下面针对最佳参数情况进行仿真,参数设置如下: Vs=220V,初级电感L=1×10-3H,初级滤波电容C1=3.3μF,输出储能电容C2=1500μF,开关管的工作频率为fS=50KHz,负载R=50Ω。
仿真结果如下:
系统进入稳态后,输入电压电流波形如图7所示。可以看出变换器输入电流很好的跟踪了输入电压的波形。为了便于比较,图中交流电压Vs幅值是原来的1/20,每一格代表20伏特,电流的单位是安培。
图7 输入电压电流波形
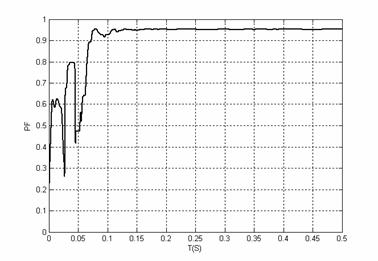
功率因数的曲线如图8所示,从图中可以看出在0.15秒以前电路处于非稳定状态,功率因数有较大跳变,在0.15秒以后电路进入稳定状态,功率因数可以达到0.95以上。
图8 功率因数的曲线
输出电压波形如图9所示,从图中可以看出输出平均电压为400V左右,通过放大后的可以看出纹波电压的峰峰值为15V,该电路电容电压被很好的限制在一定的范围内,储能电容的耐压大大减少,保证了电路的输出特性。
图9 输出电压波形
5 结论
双向开关前置的单相升压APFC变换器电路把双向开关放置在整流桥前端,较好的解决了传统单相升压APFC变换器电路置后的升压电感直流偏磁问题,也便于电路的集成。通过优化电路参数配置可以实现很高的功率因数,而且输出电压稳定,输出纹波电压低,能够获得很好的输出特性。本文通过仿真找到了比较好的参数配置范围,对实际应用具有重要的指导意义。
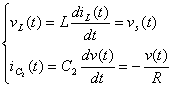 (1)
(1) 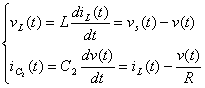 (2)
(2)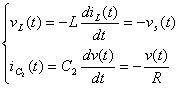 (3)
(3)  (4)
(4)![]() 、
、![]() 和
和![]() 为:
为:![]() (5)
(5)![]() (6)
(6)![]() (7)
(7)![]() (8)
(8)![]() (9)
(9) (10)
(10) (11)
(11)![]() 、
、 ![]() 外都为线性项,而且这两乘积项远小于其它项,若将它们略去,不会给分析引入太大误差,则线性化后的交流小信号状态方程为(12)、(13)。
外都为线性项,而且这两乘积项远小于其它项,若将它们略去,不会给分析引入太大误差,则线性化后的交流小信号状态方程为(12)、(13)。 (12)
(12) (13)
(13)