现代计算机系统的规模越来越庞大，越来越复杂，导致计算机系统的可靠性保障的难度也越来越大。因此，计算机系统的可靠性已为社会所广泛关注[1]。面对这种形势，国际上越来越重视软件可靠性工程理论的研究发展，将软件质量管理逐渐纳入规范化、科学化的轨道[2]。软件可靠性工程也逐渐在信息技术、可靠性工程、用户需求等综合因素的作用下发展起来，并形成了一门综合众多学科的成果以解决软件可靠性为出发点的边缘学科。
    软件可靠性工程主要研究对象为软件产品或系统的失效发生原因、消除和预防措施，以保证软件产品的可靠性和可用性，降低维护费用，提高软件产品的使用效益。软件可靠性已经成为软件业界和可靠性工程界关注的焦点、研究的热点、实践的重点。
1 软件可靠性数据
    不同的软件错误、缺陷及其故障在表现形式、性质乃至数量方面可能大相径庭，对其进行全面、详细的阐述是非常困难的，也是不客观、不现实的。但是现实中，为了简单易行，通常假设软件可靠性模型所有失效等级相同，或属于同一类，即不再区分软件错误、缺陷及其故障。如果要区分失效等级和失效类型，将随之带来很多问题。例如,同一模型是否适用于不同类型的失效数据；由于分类后各类失效数据样本一般极少，将会影响模型给出结果的精度。因此一般情况下，不再对失效数据进行分类[3]。
    经典的软件可靠性模型有:(1)1972年,Jelinski和Moranda首次提出了软件可靠性模型的概念，并建立了具体的可靠性模型——J-M模型[4-5]; (2)1973年,Littlewood和Verall采用Bayes方法进行软件可靠性测试[6];(3)1979年,Goel和Okumoto提出了改进J-M模型的非齐次泊松过程模型，即G-O模型;(4)1983年,Yamada和Osaki发现错误数在预测初期增长缓慢随后快速增长，最后趋于饱和，即延时S形增长模型，称为Y-O模型[7]。
　任意选取一组如表1所示的MUSA J M的软件可靠性数据，使用笔者开发的软件可靠性预测系统，验证上述4个软件可靠性模型，得到的拟合曲线如图1所示。由图可以看出，由于原始的软件可靠性数据间隔时间的不平稳性，导致其最终预测结果产生极大的误差，特别是在波峰波谷处。

　通过对大量软件可靠性数据的研究分析发现，软件发生缺陷的间隔时间具有较大的波动性，而这也正是导致其预测结果误差较大的主要原因。描绘其波动性趋势，构建软件可靠性数据的波动模型，是解决问题的关键。
2 软件可靠性数据的预处理
   为解决上述问题，本研究将软件可靠性数据分解成独立的两部分数据。一部分描绘软件可靠性数据的总体趋势；另外一部分描绘软件可靠性数据随时间的波动趋势。通过两部分数据的分别预测和组合，得到最终的可靠性结果。
　设软件失效间隔时间分别为：x(1),x(2),…x(n)，失效时间分别为：t(1),t(2),…t(n),其中t(i)为软件开始运行到第i次失效发生的时间,x(i)为软件第i-1次失效到第i次失效发生的时间间隔，即x(i)=t(i)-t(i-1)。
　假定t时刻的软件可靠性数据M(t)=P(t)+Q(t)，其中P(t)用来描绘软件可靠性数据的总体趋势，Q(t)用来描绘软件可靠性数据随缺陷出现的波动趋势。

    按上述算法，对表1所列数据进行处理得出表2结果。

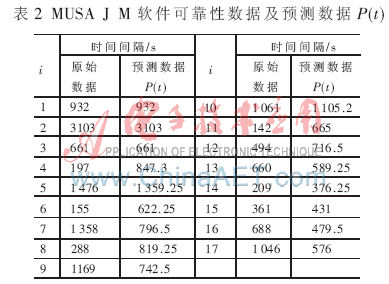
　表2所估算的预测数据P(t)的时间间隔曲线如图2所示。由图可以看出，其整个趋势相对于原始数据相对平稳,且其大致趋势与原始数据曲线趋同。

    根据原始数据与预测数据P(t)的差值曲线，寻找并预测Q(t)的变化规律。由图3可以看出，对于波动程度的取值,必须要考虑波动的正负和波动的幅度两方面因素。

　同样根据早期数据对预测未来行为作用很小，而现时失效间隔数据可以比更早之前观测的失效间隔数值更好地预测未来这个原理，本研究选取Q(t)之前的5个失效数据点进行波动值Q(t)的预测。
　首先根据之前5个点波幅4次正负切换的次数，预测时刻t相对于上一时刻t-1波幅的异号或同号的可能性。

　波动的幅度通过取5个点的振幅绝对值平均值得到。同时可以发现对于点Q(t-1)的振幅与Q(t)的预测也有较大联系，假设Q(t)=a×Q(t)+b×|Q(t-1)|，a取值0.7，b取值0.3。
　按照上述算法,将估算的P(1)…P(t-1)值代入软件可靠性模型，得到P(t)，最终得到时刻t的预测时间P′(t)+Q(t)。
3 算法验证
　(1)使用Littlewood-Verall模型对P(t)进行运算,根据P(t)…P(t-1)求得预测的P′(t),结果如表3所示。

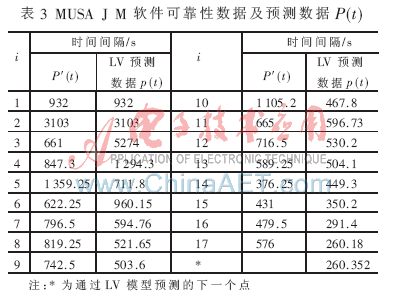
    定义可靠性模型评价标准：
   
    剔除失效数据点1、2、3，其他的14个失效数据点RE的为0.349 351,而初始的失效间隔的RE值为1.595。可见通过平稳处理失效数据点,可以得到更高的拟合度。
　(2)求值Q′(t)，按照之前算法，得到的值如表4所示。

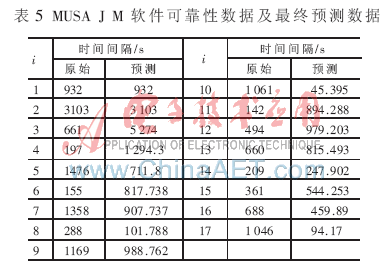
   由于前5个失效数据点的预测Q′(t)缺少有效的数据，所以计算ESS时,将其剔除，剔除后的点求得RE的值为1.23，相对于使用未经处理的点获得的RE值(1.595)误差减小近20%。同时，可以看到其产生误差的主要原因是失效数据点11所导致的。MUSA J M软件可靠性数据及最终预测数据如表5所示。

    软件可靠性评估日益受到重视，作为其核心的软件可靠性模型理论的研究也势必要深入下去。本文的研究开启了软件可靠性理论研究的入口，以后的研究除了对可靠性数据进行进一步处理外，也将对软件可靠性模型进行进一步的改进。
    本文在传统方法仅关注软件可靠性模型的基础上，拓宽至对可靠性数据的预处理,提出了一种对软件可靠性数据处理的新方法，解决了可靠性数据采集过程中出现波动性大的缺陷，而且算法简单、稳健性好,可以适用于各种工程应用。但其中还有很多问题值得进一步研究，例如，如何实现新算法中Q(t)系数的自适应等。
参考文献
[1]  孙志安, 裴晓黎. 软件可靠性工程[M]. 北京：北京航空航天大学出版社, 2009.
[2]  徐仁佐. 软件可靠性工程 [M]. 北京:北京清华大学出版社,2007.
[3]  LYU M R. 软件可靠性工程手册 [M]. 刘喜成,等译.北京:电子工业出版社, 1997.
[4]  MUSA J D, IANNINO A, OKUMOTO K. Software reliability: measurement,prediction, application[M]. New York: McGraw-Hill, 1987.
[5]  CHEUNG R C. A user-oriented software reliability model [J]. IEEE Transactions on Software Engineering, 1980,3-6(2):118.
[6]  LITTLEWOOD B. A reliability model for system with  markov structure[J]. Applied Statistics, 1975,24(2):172.
[7] GOSEVA P K, TRIVEDI K. Architecture-based approach to reliability assessment of software systems[J]. Performance Evaluation, 2001, 45(2-3):179-204.
[8]  蔡开元. 软件可靠性工程基础 [M]. 北京:北京清华大学出版社,1995.