在现阶段的软件无线电平台中，直接对射频(RF)进行采样还很难实现，成本上也很不合算。所以在目前的研究中，大部分都是首先将射频信号转换到中频(IF)上，在中频对模拟信号进行数字化，然后采用数字下变频(Digital Down Conversion，DDC) 技术，将采样率较低的信号送给后续的基带信号处理单元。
　　实现DDC主要有三种途径：(1)采用已有的专用芯片；(2)自己制作专用芯片；(3)基于FPGA或DSP等通用芯片自建平台实现DDC。但是在高采样速率的系统中，如A/D" title="A/D">A/D采样的速率为400MHz时，这三种方法显示出各自的弊端：商用专用芯片要求A/D转换器转换出的数据速率较低，比如AD6620要求数据速率小于70MHz，HSP50016要求数据速率小于75MHz；而自己制作专用芯片,由于成本过高和国内技术条件的限制，在小规模的研发生产中几乎是不可能的；用DSP芯片自建平台实现DDC时，虽然DSP可以高速执行乘加指令，但由于DSP是串行执行指令的，在高速处理中会遇到处理能力过低的问题；虽然用FPGA片内资源可以同时进行多个乘加运算，但是用FPGA片内资源实现的乘法器" title="乘法器">乘法器速度较慢，很难实现高速数据流的实时乘加处理。
　　本文介绍一种基于新型FPGA的高速数字下变频的实现方法，它充分利用数字下变频的优化算法以及FPGA领域的新技术，去除由于数据速率过高而造成的各种瓶颈，极大地减少了计算量和FPGA片内资源的消耗。
1 数字下变频算法的改进优化
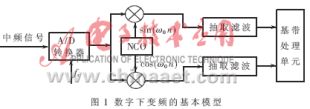
　　数字下变频的基本功能是将速率较高的数字中频信号下变频为数字基带信号,并降低信号的采样速率。图1是数字下变频的基本模型。图中将高速A/D转换器的输出信号送入数字下变频器；经两个相乘器所构成的混频器后，将输入的数字信号和复正弦信号产生器产生的正交正弦信号相乘，相乘结果为I、Q两路信号；再分别经高抽取滤波器" title="抽取滤波器">抽取滤波器和有限长冲击响应(FIR)滤波器进行处理。由这两个滤波器构成的复合滤波器的功能是低通滤波和抽取，其输出是数据流降低了的数字基带信号。

　　用FPGA实现图1所示的经典的数字下变频会遇到如下几个瓶颈：(1)当中频信号采样速率较高时(大于200MHz)，
　　FPGA无法用普通I/O引脚接收；(2)用常用的查表法无法实现高速NCO；(3)混频器用到的高速乘法器无法实现；(4)抽取滤波器中的高速乘法器和加法器实现困难。
　　解决上述问题的基本思想方法为：利用多速率信号处理理论，先抽取后处理，这样就能避开由于高速率而带来的瓶颈。
1.1 多相抽取滤波器
　　如果用传统的方法对信号进行抽取(抽取因子为D)，其过程为：先将信号输入一个L阶的线性时不变FIR滤波器进行抗混迭滤波，然后再进行抽取；如果采用多相抽取滤波器，可以实现先抽取后滤波，其过程为：先对信号进行抽取和分路，然后将抽取的结果输入各多相分支滤波器。
　　多相分支滤波器的实现方法如下：把这个L阶的抗混迭滤波器“拆分”为D个P阶的滤波器，其中P=L/D是各个分支滤波器的阶数。设原L阶滤波器的冲击相应为H(n)，n=0、1、2、…、L-1，那么每个分支滤波器的冲击响应由下式决定：
　　H_k(n)=H(k+nD)
　　式中,k表示第k支路，k=0、1、2、…、D-1;n=0、1、2、…、P-1。
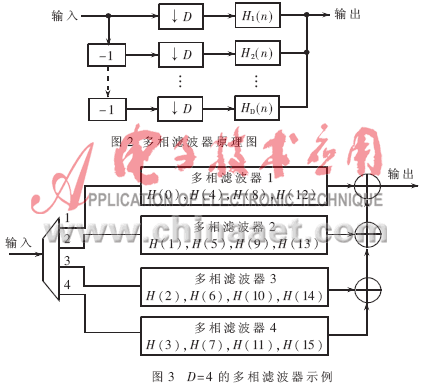
　　利用多相分解得到的多相抽取滤波器如图2所示，图3是一个具体的多相滤波器的例子。在图3中，滤波器要实现间隔为4的抽取，抽取滤波器的阶数为16，经多相拆分为4个分支滤波器。

1.2 高速NCO的等效处理
　　在数字下变频的实现中，高速NCO的实现是系统的另外一个瓶颈。下面介绍高速NCO的等效处理。
　　将0～f_s的频带作如下划分：将整个频带划分为N个信道，N=2D，D为抽取因子，设每个信道的带宽为B，B=f_s/D，相邻信道间的交叠为50%。当D=4时，信道的划分如图4所示。只要抽样速率符合奈奎斯特定理，这样划分就可以保证信号完整地存在于某一个信道内。

　　假设带通信号的调谐频率为f₀，将这个调谐频率f₀分解如下：f₀=m+fd，其中m是第m个信道的中心频率，f_d是f₀和m的频差，取m的值使得f_d最小。当信号带宽完全位于第m个信道中时，由于第m信道的中心频率为m，选择序列与输入序列相乘进行混频，然后进行抽取、多相滤波。这个过程如图5所示，混频之后的信号会带有频差f_d，因f_d较小，故可以在数字下变频之后用其它的方法进行消除。由于fd的消除并不是本文讨论的主要问题，故下面只讨论各个信道的下变频。

　　注意到Wm(n)具有以下性质：
　　当n＜D时，
　　
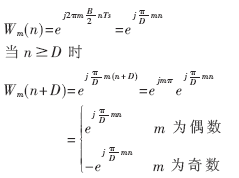
　　因此，如果信号带宽位于偶数信道内，即m为偶数，混频器序列的周期为D，那么在多相滤波器中，W_m(n)可以相应地分配给各个分支，其实现过程如图6所示。

　　如果信号带宽位于奇数信道内，即m为奇数，混频器序列周期为2D，且W_m(n)=-W_m(n+D)，那么由于输入数据在输入多相滤波器之前已经进行过间隔为D的抽取，因此可以将抽取后的数据进行模2编号，编号为0的数据不变，编号为1的数据取相反数。其具体实现框图如图7所示。

　　图7中只画出了一路分支滤波器的实现方法，其它分支滤波器的处理同理可得。
2 高速数字下变频的实现方案
　　综上所述，通过对DDC实现方法的优化，极大地减小了计算量，降低了对器件处理速度的要求，但是当信号带宽较宽时，改进算法后计算量仍然很大。比如，前端A/D转换器输出的数字信号速率为400MHz，经过抽取因子为4的抽取后，信号的速率仍然有100MHz。显然，用单片DSP很难完成抽取滤波和混频处理工作，于是用FPGA实现DDC就成了唯一选择。
　　运用FPGA片内的高速数据接口和DSP功能，结合上述优化算法，就可以有效地解决高速数据实时处理的问题。
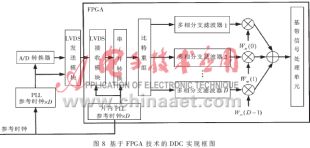
　　基于FPGA技术的DDC实现框图如图8所示。图中，系统参考时钟f_r=f_s/D。在A/D端，用PLL产生采样时钟f_s，其上升沿和参考时钟f_r的上升沿对齐。在数据接收端，FPGA内置PLL产生时钟信号驱动片内LVDS接口，这个时钟信号的上升沿和参考时钟上升沿对齐。LVDS接口接收高速差分信号，同时进行串/并转换和比特重组。串/并转换过程等效地完成了抽取工作。

　　图9(a)所示的是在Quartus II集成开发环境中调用库函数ALTLVDS实现的LVDS接收接口，其功能为：接收速率为400MHz的输入信号，并作串/并转换，以实现抽取因子为4的抽取，抽取后的数据分四路输出，速率为100MHz。图9(b)是LVDS接口的仿真波形，图中rx_in[7..0]是A/D转换器输出的数字信号，位宽为8位；rx_clock为参考时钟f_r，频率为100MHz；rx_outclock是输出信号时钟，其频率为f_r，这个时钟和输出的数据之间有固定的相位关系，这个相位关系由数据对齐方式(一般是沿对齐)指定；rx_out[31..0]为串/并转换后的输出结果，经过比特重组后，可以得到四路数字信号out1st[7..0]、out2nd[7..0]、out3nd[7..0]、out_4th[7..0]，这四路信号将分别输入四个分支滤波器。

　　抽取工作完成后，将各个支路的数据分别按时序送入相应的分支滤波器。由于FPGA的逻辑资源和寄存器资源有限，而乘法器的实现(尤其是位数较高时)比较多地耗费FPGA内部的寄存器资源，同时用逻辑和寄存器资源实现的乘法器运算速度比较慢，常常达不到建立时间和保持时间的要求，因此应该尽量利用片内专用乘法器来实现滤波器。
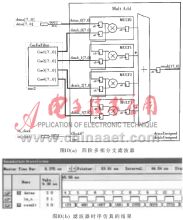
　　在Quartus II中，用户可以通过调用库函数ALTMULT_ADD来使用片内专用乘法器。图10(a)中所示的是调用ALTMULT_ADD函数生成的四阶多相分支滤波器。图中dataa[7..0]为分支滤波器的输入数据；datab_0[7..0]、datab_1[7..0]、datab_2[7..0]、datab_3[7..0]是滤波器系数。in_clock为输入数据的时钟信号，其频率为fr，同时这个时钟还控制着滤波器输出的Pipeline时序，result[17..0]为滤波器的输出数据。

　　图10(b)是时序仿真的结果，由于运用了片内硬件乘法器，运算速度大为提高。图中in_clock的频率为100MHz，在这个频率下，滤波器输出的数字信号完全可以达到建立时间和保持时间的要求。
　　用QuartusII实现DDC的顶层模块如图11所示。在实际系统中，它对如下中频信号作DDC处理：中频信号的调谐频率为100MHz，信号带宽为10MHz；前端A/D采样速率为400MHz，位宽为8位；要求产生速率为100MHz的基带信号。