1 引 言
当前,许多工矿企业使用的功率因数补偿器大部分是采用三相同时补偿的方式,这在三相负载对称或基本对称时补偿效果较好的。但现在许多用电对象是大量的不对称三相负载,如科研单位、宾馆、百货大厦、高等学校、机关等,这些单位使用大量的单相感性负载(如空调、电扇、电取暖设备、各大型照明设备、广告灯设备),虽然这些单件负载的无功损失不大,但作为整个单位或一个区域积少成多,其功率损失也不可小视。显然,对这类三相不对称负载的用电户必须采用各相分别补偿的方式提高功率因数。
在本文中,采用PIC16C72" title="PIC16C72">PIC16C72单片机实现三相不对称负载的无功补偿" title="无功补偿">无功补偿,并提出了补偿电容容量的优选算法及负载性质判定算法。
2 补偿电容容量的优选算法
为使补偿的容量选择更加合理和适用,我们对补偿的工作环境和实际情况进行测量和定性,来决定此补偿器的具体补偿容量,以达到非常合理和有效的补偿效果。
根据无功功率容量的计算表达式:
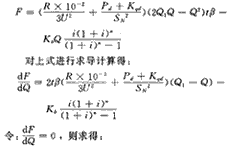
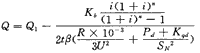
这就是无功补偿最佳容量的计算式。
其中:kb:无功补偿的综合投资率(元/kVar);
U:网络的运行电压(V);
Q1,Q2:补偿前后的无功功率(kVar);
Q:补偿装置的无功容量(kVar);
Pd:变压器的短路有功功率(kW);
SN:变压器的额定容量(kVA);
β:单位电价(元/kWh);
i:无功补偿装置综合运维费率(%),根据银行利率和折旧而定;
n:无功装置使用年限,一般以电容器寿命10年估计。
3 负载性质判定(相位测量)算法
负载性质(感性和容性)的判定决定着补偿电容的投切情况,直接影响着输电线路上的功率因数,对功率因数和用电质量的改善有着决定性作用。而负载性质又由线路中电压和电流的相位差" title="相位差">相位差决定。
因此,电压和电流相位差的准确测量决定着用电线路的无功功率计算的准确性以及投切电力电容的合理性,他对整个补偿系统都是非常重要的。
为了能够准确地测量相位,我们采用数字鉴相法。所谓数字鉴相是指通过将两路信号比相,在鉴相输出信号的正脉冲内填入高速脉冲,通过记录填入的脉冲数来测相位差。
PIC16C72单片机自身会产生高速的数字时钟脉冲,这就可以直接利用该单片机的时钟脉冲进行相位的测量。电压与电流的波形关系如图1所示。
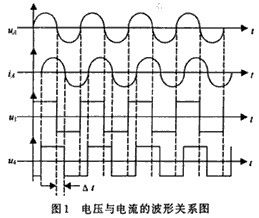
图1中A相电压UA,A相电流iA与比较器Ull,U12的输出电压波形U1,U4的关系,显然△t与U4,iA之间的相位差φA成正比,△又与u1,u4正跳变时定时器T1计数值之差△n成正比,这样只要得到△n就可得出φA的值。该系统中,PICl6C72采用12MHz晶振,定时器l每隔2/μs计1个数。定时器1是16位计数器,他从0~65 536不停的循环增1计数运行;定时器2是8位计数器,他从0~256循环计数,预、后分频各16倍,An的计算式:
△n=(B一A ×256)+65 53× N
其中:A为u1发生正跳变时定时器的值;B为u4发生正跳变时的定时器的值;N为2个事件发生的间隔期间定时器的溢出次数。
因此△n为:
△t=△n ×2 ×10-6(s)
因为△n的最小值小于5ms(工作信号的1/4周期),而T1从0~65 536计数的时间是:
65 536 ×2 × 10-6 (s)=131.072(ms)
因而在u1发生正跳变到u4发生正跳变之间T1溢出的次数最多为1,即N只有2个取值:0和1,电压uA与电流iA的相位差φA为:

根据保持寄存器和时间寄存器记录的8次事件可得出4个φA值,经过数据中值滤波、平均值滤波即可得到较准确的φA值。再通过查表法得到A相功率因数COSφA。同理控制多路模拟开关可测出B相,C相的相位差和功率因数。
4 投切容量控制算法
当测得相位差φA,φB,φC后,根据正负判断可得知是感性负载还是容性负载,感性负载时要投入电容器,容性负载时要切除电容器,投切的电容量根据测得的电压、电流值的大小来确定。图2是电容负载的等效电路和相量图,φ1是电容未投入时的相位差,φ是投电容后的电位差,I1是负载的电流(即电容未投前补偿器测得的交流电流的i1相量),Ic是投上电容中流过的电流。由相量图可知投上电容后φ最好为0,补偿以此为根据计算需投入的电容值,由向量图可得出:
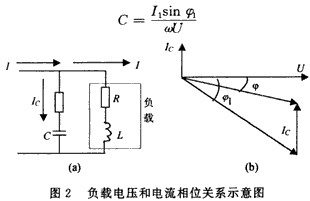
若每组待投入电容的容量为Co,则需投入电容值的组数K为:
K=C/Co (小数点后舍去)
根据K值,可一次将需投入的电容(X组电容)同时投合上.同理,若是出现容性状态,须切除的电容值为:
目前有许多补偿器是步进投切电容的,具有投切时间长、有出现振荡的可能。而采用上述算法求出投切电容的组数后,即可一次完成投切并且不会发生振荡。
5 算法的实现
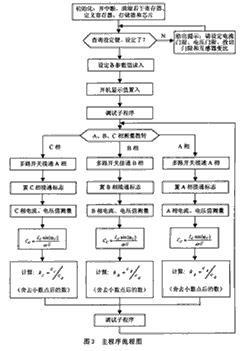
该算法可用PIC16C72单片机来实现。其主程序流程图如图3。在所有初始化以后,主程序将执行对电压和电流的测量。电压和电流的测量由PIC16C72单片机控制,分别对A,B和C三相电路测量和记录。测量值送入对应的寄存器中暂存,供以后计算子程序使用。在对每一相电路测量后,主程序还要进行投切电容量和投切电容组数的计算,所需计算参数从溢出中断子程序的计算结果中调用。
6 结 语
采用上述补偿和控制算法后,电力系统" title="电力系统">电力系统的相位测量精度可达0.5%,补偿结果能使COSφ0.95。当然这还与每组补偿电容的大小相关,若每组补偿的容量小一些,则还能提高COSφ,但相应的接口和投切控制硬件都要增加。
在实际应用当中,必须根据用户的用电情况综合分析,方可得出较为合理的安排。

