在数字信号处理领域,离散时间系统的输出响应,可以直接由输入信号与系统单位冲激响应的离散卷积" title="卷积">卷积得到。离散卷积在电子通信领域应用广泛,是工程应用的基础。如果直接在时域进行卷积,卷积过程中所必须的大量乘法和加法运算,一定程度地限制了数据处理的实时性,不能满足时效性强的工程应用。本文从实际工程应用出发,使用快速傅里叶变换(FFT)技术,探讨卷积的高速硬件实现方法。
1 卷积算法的原理
设线性时不变系统的冲激响应为h(n),则冲激响应和输入δ(n)之间有关系
![]()
假设该系统的输入为x(n),输出为y(n),则根据线性时不变系统的定义,有
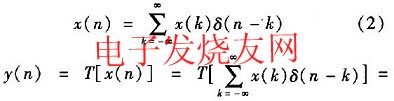

根据式(3),线性时不变系统的输出信号可以由输入信号与单位冲激响应的卷积求得。实际应用中,x(n)与y(n)的序列长度均为有限的,假设均为N,显然,求出N点的y(n)需要N2次复数乘法,当序列长度大时,所需计算量是庞大,在需要实时处理的系统中,难以满足实时性要求。
将M点序列x(n),L点序列h(n)分别作扩展,构造新的序列x’(n),h’(n),使得长度N满足如下条件
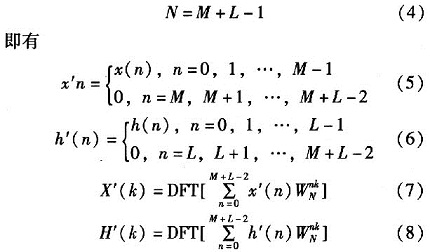
根据时域循环卷积定理,x(n)与h(n)的线性卷积可以用循环卷积来代替。即
![]()
根据式(9),给出了一种基于快速傅里叶变换(FFT)的卷积的实现方法,如图1所示。分别对补零后的z(n)和h(n)进行FFT运算,得到对应的频域响应X(k)和H(k),将X(k)和H(k)相乘的结果再做IFFT,即可以得到x(n)和h(n)的卷积结果y(n)。
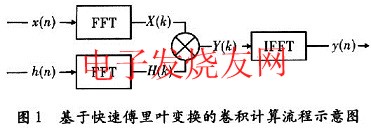
2 基于FPGA" title="FPGA">FPGA的高速卷积的实现
随着电子技术的发展,现阶段FFT硬件实现的方法主要有ASIC,DSP和FPGA这3类。专用FFT处理芯片ASIC,例如PDSPl6510,这类芯片的主要特点是技术简单。但是由于此类ASIC处理点数有限,实现大点数FFT时,需要多芯片并行工作,会导致所需的配套控制复杂、存储芯片较多,加大了系统实现难度。使用DSP,如TMS320DSP6416,控制程序设计比较简单,但由于DSP的串行式软件工作机理,当点数较大时,处理速度难以满足实时要求。使用FPGA实现FFT功能,其并行处理机制允许FFT运算过程中使用流水线的形式,大大提高处理速度,而且随着技术发展,FFT IP核技术日臻完善,使得基于FFT IP核的系统在速度、灵活性等方面均展现出优越性。本文使用Altera公司的StraTIx II系列芯片EP2S60实现线性卷积的功能。
Stratix II是Altera公司生产的一款高性能FPGA器件。它采用台积电的90 nm工艺技术生产,等效逻辑单元(LE)最高可达180 kB,嵌入式存储器容量最高可达9 MB。该器件不但具有较高的性能和密度,而且还针对器件总功率进行了优化,同时可以支持高达l Gb/s的高速差分I/O信号,因而是一款高性能的FPGA。该芯片中所含的高性能嵌入式DSP块的运行频率高达370 MHz。另外Stratix II还有12个可编程PLL,并具有完善的时钟管理和频率合成能力,能满足高性能系统的需求。
EP2S60集成了60 440个等效逻辑单元(LES),内嵌M512 RAM模块329个,M4K RAM模块255个,M-RAM模块2个,总存储单元2 544 192 bit,并集成了DSP模块36个、18 bit×18 bit嵌入式硬件乘法器144个,含有2个增强性锁相环和8个快速锁相环,可满足本系统的要求。
3 FFT IP核的实现方法
为了节省开发时间,加速产品的投放,本文使用Ahera提供的FFT IP核来实现FFT和IFFT功能。Ahera FFT IP核函数是一个高性能、参数化的快速傅里叶变换(FFT)处理器,完全支持Ahera的FPGA系列。可以完成变换长度为2m(6≤m≤14)的基2、基4按照频率抽选的高性能复数FFT以及逆FFT运算。
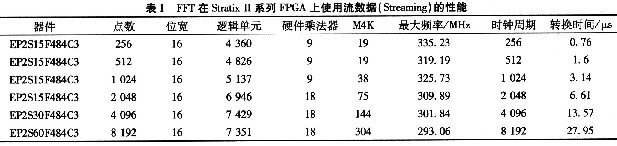
FFT IP核支持3种数据流模式,流模式(streaming)、缓冲突发模式(Buffered Burst)、突发(Burst)模式。并可以参数化设置变换点数和FFT或IFFT转换方向。表l给出了FFT在Stratix II系列FPGA上使用流模式(Streaming)的性能。
为了在整个转换计算过程中保持高信噪比,FFTIP核在定点结构与全浮点结构之间折中,使用块浮点结构来表示转换结果。在定点结构中,数据精度需要足够大,才能充分表示整个计算过程中的所有的中间计算结果。在执行定点FFT过程中,经常出现数据的位数过大或精度损失的现象。而在浮点结构中,每个数用单独的指数和尾数来表示,虽然这样可以大大提高数据精度,但是浮点运算需要占用更多的器件资源。块浮点结构保证了FFT整个转换过程中数据位数的有效使用,每次通过基4-FFT运算以后,数据位数最大可能增加倍,根据前面输出数据模块动态范围的测量进行比例换算,换算过程中累计的移位次数被作为整个模块的指数输出。这种移位方法保证了最低位(LSB)的最小值在乘法运算后的输出进行舍入操作之前就被舍弃。实际上,块浮点表示法起到了数字自动增益(AGC)的作用,为了在连续输出模块中产生统一的比例,必须用最终的指数对FFT函数输出进行比例换算。
4 实际工程中的卷积的实现
如图2所示,给出了一个实际应用的例子。为了保证I,Q两路的相位同一性,使用双通道A/D,选择Linear公司的LTC2280,LTC2280支持10 bit,105 Ms/s的最大采样率,并拥有61.6 dB的信噪比(SNR),85 dB的无杂散动态范围(SFDR),满足系统需要。双通道D/A使用Analog公司的AD9763,AD9763支持10 bit、125 Ms/s的最大采样率。

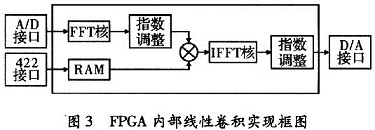
首先,需要在PC机上准备好h(n)对应的DFT变换结果H(k),H(k)的处理实际上有两种方法,一个是将h(n)下载到下位机中,使用下位机硬件实现H(k),还有就是将H(k)在上位机就计算好,直接将计算结果下到下位机中。由于h(n)在系统工作中是不变的,在PC机端事先计算好H(k)更合适,不仅可以减少FPGA的资源占用,而且也方便数据的处理。基于以上的考虑,本系统将在PC机端求出的H(k)通过422接口下载到下位机的RAM中,方便使用。
下位机系统工作之前,上位机需要通过PCI控制板卡将计算好的数据下载到下位机的RAM中,方便工作过程中的数据使用。在收到外部控制信号后,下位机开始启动,LTC2280开始采集I、Q通道数据并送入到FPGA中。
AD输出的I,Q数据直接作为一个复数的实部和虚部进入FFT核进行FFT变换。为了加速处理速度,使用基-4四引擎输出结构。FFT核输出的结果X(k)过指数调整以后直接进入到一个硬件复数乘法器,与存储于RAM中计算好的H(k)对应相乘,同时乘法器输出可以直接输入到IFFT模块进行逆FFT运算,IFFT计算结果再经过指数调整以后即可以直接通过D/A输出。
5 性能分析与改进
FPGA的流水线结构决定了速度的瓶颈取决于整个流程中处理速度最慢的部分。在FFT核速度可以保证的前提下(EP2S60的理论速度可以达到293.06 MHz),而处理过程中全部使用FPGA内部RAM来存储中间数据,所以在本系统中,FPGA内部的理论处理速度达到200 MHz以上。本系统的处理速度主要局限于A/D和D/A的数据转换率,根据实际测试,在100 MHz系统时钟下,数据吞吐率可达100 Ms/s,满足了设计技术指标。图4给出了FPGA的资源占用。为了较好地检测整个使用FFT_IFFT实现卷积的系统性能,设计了一个初略性能分析测试结构,如图5所示。

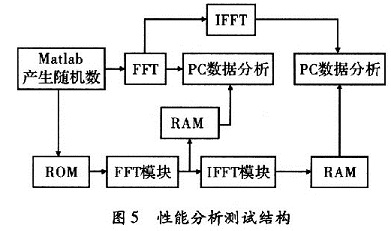
在图5中,由上位机产生的一组8 192点随机复数a(t)写入ROM中,作为FFT模块的信号输入,经过FFT后将结果B(ω)存入RAM中,以方便上位机读取并与a(t)使用Matlab计算出来的FFT结果A(ω)进行比较;接着将该FFT结果B(ω)再进行IFFT计算,由数字信号处理理论可知,一个信号进行FFT后再进行IFFT的结果应该是信号本身,所以将B(ω)再进行IFFT计算后得到的结果b(t)存入RAM,由上位机读取并与原始信号a(t)进行比较,可以分析整个卷积系统的处理误差。图6给出了计算FFT结果相对误差的Matlab相关程序。

求出A(ω)的最大值max[A(ω)],分别对B(ω)的实部和虚部计算相对误差,得到如图7所示的相对误差曲线。由图6可知,在FFT过程中,相对误差可以保证在0.5%以内。对FFT所得的结果B(ω)做IFFT得到b(t),分析b(t)与原数据a(t)的误差,得到如图8所示的相对误差曲线。

观察图8可知,经过FFT变换和IFFT变换以后的累积相对误差保持在±3%以内,主要原因是FPGA计算FFT和IFFT过程中由于精度的要求,进行数据舍去,造成误差的产生。这种误差是由硬件客观条件限制的,不可避免,但是±3%的误差精度完全可以满足实际应用。

本系统由于涉及到高速A/D、高速D/A,所以在PCB设计过程中必须考虑电磁兼容EMC(Electro MagneTIc Compatibility)和抗电磁干扰EMI(Electro Magnetic InteRFerence)性和信号的完整性。总体来说,在进行高速PCB设计过程中,不仅要考虑PCB的元器件布局和布线,同时设计中的接地、去耦和旁路同样重要。例如在A/D部分这种混合信号PCB设计中,由于混合了模拟信号与数字信号,只有尽可能减小电流环路的面积才能降低数字信号与模拟信号之间的相互干扰。一个可行的方法是将地平面分割,然后在A/D转换器下面将模拟地和数字地连接在一起。
在处理FFT和IFFT核的指数问题时,正常做法是在FFT结束后直接做一次指数调整,在IFFT结束后再做一次指数调整。设经过FFT核后的直接输出结果为X’(k)、对应指数输出为(-expl),x(n)的真实结果为X(k),则有

由式(12)可知,FFT和IFFT的两次指数调整实际可以在IFFT合为一次,可以减少控制的复杂程度。两次调整指数的示意图如图9所示。一次调整指数的示意图如图10所示。


6 结束语
本文基于Altera的FPGA EP2S60F1 020C8,搭建了结合A/D,D/A等功能的配套处理平台,完成了对高速离散卷积的硬件实现,使该系统在100 MHz时工作正常,满足了设计要求。

