摘  要： 提出了径向基函数神经网络应用于变速箱齿轮故障诊断的基本方法。利用Matlab神经网络工具箱对变速箱齿轮进行故障诊断仿真，并创建RBF神经网络与BP神经网络来进行故障诊断。通过对比诊断结果，证明RBF网络在诊断精度、诊断速度上均优于BP网络，说明RBF网络应用于齿轮的故障诊断准确、可靠，在机械故障诊断方面具有广泛的应用前景。
关键词： 故障诊断；神经网络；RBF网络；变速箱齿轮

    由于汽车的特殊运行条件和环境，以及汽车行驶过程中经常性换档，使得变速箱中齿轮、轴、轴承等常发生故障。据统计，由齿轮失效引起的汽车变速箱故障占全部原因的60%。在这里，齿轮失效的主要形式有齿根裂痕和弯曲疲劳引起的断齿等。因而随着汽车技术的发展，对变速箱实施故障诊断、特别是对齿轮的诊断变得尤为重要。目前，故障诊断技术已进入到智能化阶段。对汽车变速器齿轮故障诊断的实施方法有很多种，如磨损残余物分析诊断法、振动监测技术诊断法、声发射技术诊断法、光纤传感技术诊断法、人工神经网络技术诊断法等[1]。
    神经网络技术的出现，为故障诊断问题提供了一种新的解决途径。近几年，RBF神经网络大量应用于机械故障诊断，如汽车发动机、压缩机、水轮机、内燃机等。在故障诊断的应用中，RBF神经网络的应用能准确、快速地判断故障类型和原因，对及早发现和排除故障发挥了很好的作用。在实际运行中，引起故障的原因很多，不同故障表现出的征兆有时具有相似性。针对故障原因与故障征兆之间的非线性关系，应用RBF神经网络进行故障诊断能准确、快速判断故障类型和原因，对于提高安全性具有重要的意义。
    本文提出了RBF网络应用于变速箱齿轮故障诊断的基本方法，利用Matlab神经网络工具箱对变速箱齿轮进行故障诊断仿真，并创建RBF神经网络与BP神经网络来进行故障诊断。
1 神经网络故障诊断原理[2]
    神经网络是由多个神经元按一定的拓扑结构相互连接而成。神经元之间的连接强度体现了信息的存储和相互关联程度，且连接强度可通过学习加以调节。神经元模型结构如图1所示。

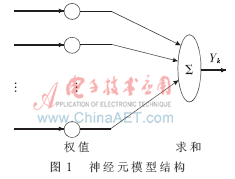
    神经网络输入层从监控对象接收各种故障信息及现象，并经归一化处理，计算故障特征值为：X=[x1，x2，…，xn]；中间层从输入得到的信息经内部学习和处理，转化为有针对性地解决办法，该层含有隐节点，一般可以完成输入模式到输出模式的非线性映射；输出层通过神经元输出与阈值的比较得出诊断结果。输出层节点数为故障模式的总数。若第j个模式的输出为：Yj=(0，0，…0，1，0…，0，0)，即第j个节点的输出为1，其余输出均为0，它表示第j个故障存在(输出0表示无故障)。
    利用神经网络进行故障诊断的基本思想是：以故障特征作为神经网络输入，诊断结果作为神经网络输出。首先利用已有的故障诊断征兆和诊断结果对神经网络进行离线训练，使神经网络通过权值记忆故障征兆与诊断结果之间存在的对应关系；然后将得到的故障征兆加到神经网络的输入端，就可以利用训练后的神经网络进行故障诊断，并得到相应的诊断结果。
    可以看出，神经网络进行故障诊断是利用它的相似性、联想能力和通过学习不断调整权值来实现。给神经网络存入大量样本，神经网络就对这些样本进行学习。当n个类似样本被学习后，根据样本的相似性，把它们归一为同一类的权值分布。当第n+1个相似样本输入时，神经网络会通过学习来识别它的相似性，并经权值调整把这n+1个样本归入一类。神经网络的归类标准表现在权值的分布上。当部分信息丢失时，如n个样本中丢失了n1(n1<n)个，则神经网络还可通过另外n-n1个样本去学习，而不影响全局。
    设对神经网络输入具有对应关系的两组样本为X(p)→Y(p)，X(p)代表输入的故障信息，Y(p)代表输出的解决策略。在这里，输入的样本越多，它的功能就越强。当有另一故障输入时，如X=X(r)+V，式中，X(r)是样本之一，V为偏差项。神经网络经过学习不断调整权值，就可以输出Y=Y(r)，这样，当输入一个新的故障现象，神经网络经过学习总可以找到一个解决策略。
2 RBF神经网络
    径向基函数(Radial Basis Function)神经网络是由J.Moody和C.Darken在20世纪80年代末提出的一种神经网络，它是具有单隐层的三层前馈网络。RBF网络模拟了人脑中局部调整、相互覆盖接受域(或称感受域，Receptive Field)的神经网络结构，已证明RBF网络能任意精度逼近任意连续函数。RBF网络的学习过程与BP网络的学习过程类似，两者的主要区别在于各使用不同的作用函数。BP网络中隐含层使用的是Sigmoid函数，其值在输入空间中无限大的范围内为非零值，因而是一种全局逼近的神经网络；而RBF网络中的作用函数是高斯基函数，其值在输入空间中有限范围内为非零值，因而RBF网络是局部逼近的神经网络。RBF网络是一种三层前向网络，由输入到输出的映射是非线性的，而隐含层空间到输出空间的映射是线性的，前者是一个非线性优化的问题，求解方法较复杂，目前可选用的学习方式较多，主要有随机选取RBF中心(直接计算法)、无监督学习选取RBF中心(K-均值聚类法)、有监督学习选取中心(梯度下降法)和正交最小二乘法(OLS)等[3-5]。本文主要采用第一种方法。RBF网络结构如图2所示。

  
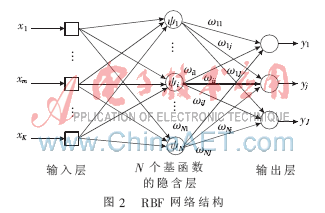
    在RBF网络训练中，隐含层神经元数量的确定是关键，一般选取与输入向量的元素相等。然而，在输入矢量很多时，过多的隐含层单元数使网络结构复杂化，影响训练时间。为此提出了改进方法:从0个神经元开始训练，通过检查输出误差使网络自动增加神经元。每次循环使用，使网络产生的最大误差所对应的输入向量作为权值向量w，产生一个新的隐含层神经元，然后检查新网络的误差，重复此过程直至达到误差要求或最大隐含层神经元数为止。
3 实验分析
3.1 RBF神经网络与BP神经网络训练过程
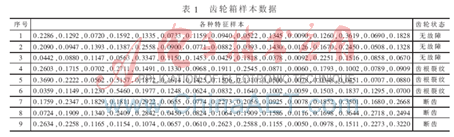
    表1为某汽车变速箱的齿轮啮合频率样本数据。这些数据都是经过归一化处理后的样本数据，共有9个实际样本，3种故障模式，每个样本有15个特征参数[6]。应用Matlab提供的神经网络工具箱构建RBF网络与BP网络，并用表1学习样本进行训练。因此，可按照如下的方式设计网络，网络的输入层神经元个数为15，输出层的个数为3个。由于齿轮包括3种故障模式，因此可以用如下形式表示输出：无故障(1，0，0)；齿根裂纹(0，1，0)；断齿(0，0，1)。

    利用函数newrb创建一个精确的RBF神经网络，该函数在创建RBF神经网络时，自动选择隐含层的节点数目，使得误差为0.001。代码为:
    net=newrb(x，y，0.001，0.9，15，1)；
其中，x为输入向量，y为目标向量，它们可以从表1中得到。径向基函数的扩展速度SPREAD，经不同值的试验确定为0.9，神经元的最大数目为15，两次显示之间所添加的神经元数目为1。由于网络的建立过程就是训练过程，因此得到的网络已经是训练好了的。
    根据经验公式估计BP网络有10个隐层节点，其中隐含层神经元的传递函数为tansig，输出层神经元的传递函数为purelin，选用一种学习效果较好的动量及自适应学习率算法traingdm。两种网络的目标误差设为0.001，对应各自网络的误差平方和与训练步数的变化曲线如图3和图4所示。

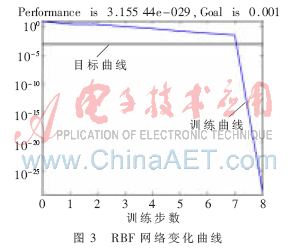
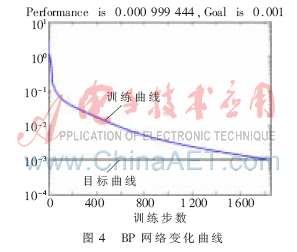
    由图3、图4可知，在达到规定的期望误差平方和的前提下，BP网络所需的训练步数约1 847步，RBF网络只需8步。RBF网络训练速度快，可以在很短的时间内诊断出故障，完全能够达到实时诊断的要求。
    RBF网络的误差为:
    NEWRB，neurons=0，sse=3.617 45
    NEWRB，neurons=2，sse=2.755 72
    NEWRB，neurons=3，sse=1.223 87
    NEWRB，neurons=4，sse=0.537 735
    NEWRB，neurons=5，sse=0.179 913
    NEWRB，neurons=6，sse=0.092 184 5
    NEWRB，neurons=7，sse=0.035 904 2
    NEWRB，neurons=8，sse=3.155 44e-029
    BP网络的误差为:
    MSE=9.994 4e-004
    由误差结果可知：RBF训练过程中，隐含层的节点个数(neurons)是从0开始，中间通过检查输出误差(sse)与目标误差(goal)的偏差值，使建立的网络自动增加神经元个数(建立网络时设定每次只增加1个神经元)，直到均方误差满足要求为止(sse=3.155 44e-029<goal=0.001)。可见RBF网络的建立过程即为网络的训练过程，且网络收敛幅度大，速度快。相比BP网络，精度更高。
3.2 故障诊断推理
    首先验证RBF网络的预测性能。代码为:

    ty=sim(net，tx)
   
其中tx为网络的测试样本。
    三层RBF神经网络进行故障诊断，采用数据驱动的正向推理策略，从初始状态出发，向前推理，到达目标状态为止。其故障诊断结果如表2所示。

    抽取表2所示的3组新数据作为输入数据，对已经训练好的网络进行测试。其测试结果为：
  
    也就是说，将第一组测试数据(无故障)输入网络时，网络输出有ty1=(1.007 3，-0.004 7，-0.002 6)，所以网络诊断的结果为无故障；将第二组测试数据(齿根裂纹)输入网络时，网络的输出有ty2=(-0.032 4，0.993 8，0.038 6)，所以网络诊断的结果为齿根裂纹；同样，将第三组测试数据(断齿)输入网络时网络的输出有ty3=(-0.008 9，0.004 7，1.004 2)，所以网络诊断的结果为断齿。
    BP网络的测试结果为:
   
    从结果来看，应用RBF神经网络对变速箱的齿轮故障进行诊断明显优于应用BP神经网络，达到了应用RBF网络进行故障诊断研究的目的。
    仿真试验表明，RBF神经网络是一种性能良好的非线性逼近网络，对故障类型的识别十分准确。网络训练过程中，在采用相同的输入节点、输出节点，且在相同期望误差平方和的条件下，RBF网络的收敛速度明显高于优化的BP网络，不仅减少了样本的学习时间和复杂度，而且不容易出现局部极小值。通过对比可知，采用RBF网络对变速箱的齿轮进行故障诊断是可行的，并且RBF网络比BP网络诊断速度快且准确，更适用于进行故障诊断。这种故障诊断方法不仅可用于变速箱齿轮故障诊断，也完全可用于柴油机、大型旋转机组等的故障诊断，因而具有广泛的应用前景。
参考文献
[1] 金鑫，任献彬，周亮.智能故障诊断技术研究综述[J].国外电子测量技术，2009(7):30-32.
[2] 马杏斋，冯志杰.热工动态过程故障的模糊神经网络诊断方法研究[J].电子测试，2007(5):59-62.
[3] 宋宏儒，丁常富，冯玉朝.RBF神经网络在高加故障诊断中的应用[J].东北电力技术，2008(11):15-18.
[4] HAGAN M T， DEMUTH H B， BEALE M. Neural network design[M]. PWS Publishing Company， 2002.
[5] 蒋良孝，李超群.基于BP神经网络的函数逼近方法及其MATLAB实现[J].微型机与应用，2004(1):52-54.
[6] 袁科新，刘枚.神经网络在故障诊断中的应用[J].山东商业职业技术学院学报，2006(8):97-99.