快速高效的半像素运动估计算法的VLSI实现
2008-10-31
作者:鲍 林 李维祥
摘 要: 提出了半像素运动估计" title="运动估计">运动估计算法的硬件实现方案,该方案可有效地提高视频编码的速度,耗费较低的硬件资源,减小处理器的面积。
关键词: 半像素运动估计 视频压缩
1 运动估计和运动补偿
在视频压缩编码中,当编码器对图像序列中的第N帧进行处理时,利用运动补偿中的核心技术——运动估值ME(Motion Estimation),得到第N帧的预测帧N’。在实际编码传输时,并不总是传输第N帧,而是第N帧与其预测帧N’的差值⊿。如果运动估计十分有效,⊿中的概率基本上分布在零的附近,从而导致⊿比原始图像第N帧的能量小得多,编码传输⊿所需的比特数也就少得多。这就是运动补偿技术能够去除信源中时间冗余度的本质所在[5]。
2 整像素运动估计
在获得运动矢量的方法上有着很多的标准和技术。其中平均绝对误差MAE(Mean Absolute Error)在精确程度和计算复杂度之间是一个很好的折衷(还有很多其他的标准,例如:CCF、MSE、SAD、SAD summation truncation、SAD estimation、PDC、MME、RBMAD、ABT、DPC、MADM)。如果使用MAE标准,对于一个确定的向量vector (i, j),两个宏块" title="宏块">宏块之间的偏差定义为:
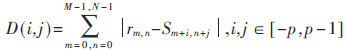
其中r是参考宏块,s是候选坐标宏块。参考宏块的大小为M×N, 候选宏块的大小是(N+2p-1)(M+2p-1)。让D(i,j)达到最小的就是运动矢量。如果参考宏块与所有的搜索区域内的候选宏块比较,这个过程就叫做全局搜索匹配算法FSBMA(full-search block matching algorithm,实现方法参见文献[2])。例如,在32×32的搜索块中,参考宏块16×16,则共算出289(=17×17)个D(i,j),让D(i,j)达到最小的就是运动矢量。
3 半像素运动估计
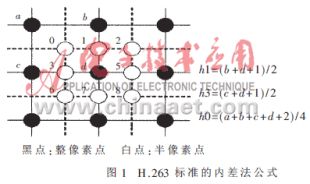
许多视频应用中都会需要一些亚像素运动估计,如半像素或者是四分之一像素估计。分数像素的像素估计将会有更好的图像预测效果。半像素估计是在先前最好的整数像素估计上继续操作。搜索区域是目标周围的区域。像素值的插值" title="插值">插值由周围的在这个范围中间的像素一起计算得到。插值中一般采用线性插值" title="线性插值">线性插值的方法。图1是H.263标准的内差法公式。
计算出整像素最优的运动矢量后,在其附近进行插值,然后再比较得出的新最优的运动矢量。流程如下:
·从前一个模块输入计算得到的整像素的运动矢量;
·在此运动矢量附近进行半像素插值" title="像素插值">像素插值,插值时只需要原先最优的宏块和这个宏块周围的一圈像素来进行插值。 这样除了原先的宏块,另外在每个像素点的附近又插值出8个半像素点,这些对应的半像素点构成了8个相同规模的宏块;
·在插值后,将新的8个模块与原始参考模块进行比较,计算出8个SAD(累计误差和)。然后比较出最优的匹配宏块,输出计算结果。 最后再将最优的与原先整像素的最优比较,输出其中最优的结果。
4 VLSI实现
本设计提出的计算半像素运动估计的体系结构中,设所使用的参考宏块为(N-2)×(N-2)的像素矩阵,那么经过全搜索方式得到最佳匹配模块后,再经边缘扩展,共有N×N个整像素点,这些像素点作为半像素插值模块的输入数据,逐行串行输入进行处理。本文具体讨论半像素插值和半像素运动估计的硬件实现,对于前级的整像素运动估计和边缘扩展的实现方法不作具体讨论。
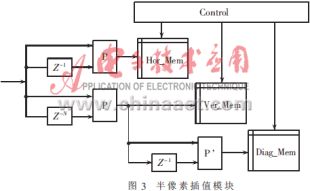
本文所提出的体系结构如图2、图3所示,模块P为线性插值模块,将两个输入数据的线性插值输出。P’的输出为两输入数据的中值,P’是通过已得到的纵向插值来计算斜向插值的模块。在线性插值的计算中,对横向插值、纵向插值和斜向插值分别计算,其中Hor_Mem存放横向插值(如图1中的点3,5),该存储器的深度为(N-2)×(N-1);Ver_Mem存放纵向插值(如图1中的点1,7),该存储器的深度为(N-1)×(N-2);Diag_Mem存放斜向插值(如图1中的点0,2,6,8),该存储器的深度为(N-1)×(N-1)。

原始的N×N个整像素点逐行串行输入横向插值模块,该模块将每两个相邻像素点的线性插值输出,结果存到Hor_Mem中。但每行(即N个像素点)输入结束时,最后一个线性插值结果应该忽略,因为该值是由本行最后一个点和下一行的第一个点插值而来,这个值是没有意义的,并且在插值结果中,第一行和最后一行也应舍弃掉,因为它们不是半像素插值点。反映到数据流中,这个过程就是将开始的连续N个输出结果丢弃,然后每N个点舍弃一个点,最后将结束的连续N点丢弃。这个过程可以通过Control模块来控制Hor_Mem的write_enable完成。
对于纵向插值,可以这样得到:不难想象,纵向插值即为当前像素点与该点前面的第N个点的插值,这样可以对输入数据做N个时钟周期的延迟,再与当前像素点作线性插值。对于这个插值结果,同样需要丢弃一些数据。首先,开始的N个插值结果需要丢弃,因为输入的第一行数据的前面N个值是不存在的,所以这N个插值结果是没有意义的。对于插值结果的首尾两列也应舍弃掉,因为它们不是半像素插值点。反映到数据流中,这个过程就是将开始的连续N个输出结果丢弃,然后每N个点舍弃首尾两点。这个过程同样由Control来控制。
对于斜向插值,其计算公式为h0=(a+b+c+d+2)/4,将其变换成h0=((a+b+1)/2+(c+d+1)/2)/2。于是不难发现,斜向插值即为与其相邻的两个纵向(或横向)插值结果的中值,这里选用纵向插值作为输入,因为连续两个纵向插值即可求出一个斜向插值来,这样只要将纵向插值结果串行输入到P’模块即可。同样,对于输入到Diag_Mem存储器中的数据,同样需要取舍:首先前N个纵向插值没有意义,那么前N个斜向插值自然也会舍掉,然后每行的最后一个中值结果也要舍掉。因为这个结果是隔行算出的中值结果,显然没有意义。
这样所有的插值结果都已经计算出来并存在三个存储器中,那么接下来就可以计算这些半像素插值的累计误差和(SAD),其中通过Hor_Mem算出2个水平运动的SAD,Ver_Mem算出2个垂直运动的SAD,Diag_Mem算出4个斜向运动的SAD。对于计算SAD的过程,有两种选择,可以用一个计算累计误差和的模块顺序逐一计算出这8个SAD,这样做可以节省硬件资源,但是缺点也很明显,输出结果要等到8个SAD计算完之后才能输出,延迟过长,影响整体编码的速度和效率。相应地,还可以用多个SAD模块并行计算累计误差和,对水平、垂直、斜向的累计误差和分别同时计算,这样提高了编码效率,但这是以硬件资源为代价的。总之,在计算完插值后,作半像素运动估计时,要根据具体的应用需求和硬件资源进行相应的取舍。
5 关于存储器
对于存储器的设计,同样面临两种选择:一是选择单口RAM,这样只有等到半像素插值点全部计算完毕并且已经存在三个存储器中,才可以读取RAM中的数据来计算接下来的8个累计误差和,这样做对于单口RAM的设计来说,实现起来比较简单,可以节省硬件资源,但是同样也会带来较大的时间延迟;二是选择双口RAM,这样对三个存储器的读写可同时进行,随着半像素插值点不断存入存储器,累计误差和模块同时也在对已有的半像素插值点计算累计误差和。这样实现了流水线设计,减小了整体延时,当然这仍旧是以硬件资源为代价的。首先双口RAM的逻辑设计要比单口RAM消耗更多的逻辑资源,而且累计误差和模块要通过复制来并行处理三个存储器中的数据,这些都会增加硬件的负担。
既然两种方法利弊明显,笔者在这里提出一种折衷的方案:设算出一个累计误差和的时间为TS,那么从4个斜向运动估计的累计误差和的计算总共需要4TS的时间、而水平、垂直运动的累计误差和分别只需要2TS的时间,那么即使采用流水线的实现方案,也要等到4个斜向SAD算出之后才能对8个SAD值做出比较。也就是说,有水平、垂直的累计误差和模块要闲置2TS的时间,硬件资源的利用率没有得到完全发挥。于是采用一种折衷的方案,Hor_Mem、Diag_Mem采用双口RAM,以流水线的方式完成累计误差和的计算,而Ver_Mem则采用单口RAM的方式实现,并且水平垂直的累计误差和的计算将复用同一个模块,即先算出水平运动的2个SAD,然后再算垂直运动的2个SAD,这样可以与斜向运动的4个SAD值的计算同步完成。
6 时序分析
原始的N×N个整像素点矩阵串行输入,这要花费N2个时钟周期,半像素插值点的计算是随着整像素点的输入同时进行的,在这N×N个数据输入结束时,所有的半像素插值点也已经计算完毕,存储在三个Mem中。接下来的时序要根据运动估计模块来分析,如果只用一个计算累计误差和的模块逐一计算这8个SAD,假定每个模块耗时(N-1)2个时钟周期,那么整个过程总共耗时N2+8×(N-1)2个时钟周期。假定时钟频率为100MHz,搜索模块大小为32×32,那么N=34,计算得到总时间约为0.1ms,完全可以满足大多数的视频压缩需求。而如果采用双口RAM,并且通过对累计误差和模块的复制来提高速度,那么编码时间还会大大降低。
本文提出了一个实现半像素运动估计的VLSI的体系结构,这个算法模型包括:累计误差和模块、线性插值模块,控制模块(即存储器的地址发生器)和三个存储器模块、每个模块的实现都很简单,只需要一些加法器、计数器、移位操作和一些简单的控制电路。本设计方案已经用行为级verilog实现成功,综合后的工作频率为200MHz,其关键路径由存储器的数据访问速度决定。
参考文献
1 T. Toivonen. Number Theoretic Transform -Based Block Mo-tion Estimation. Master′s Thesis. University of Oulu.Finland (2002)
2 H. A. Mahmoud, M. Bayoumi.A Low Power Architecture for a New Efficient Block-Matching Motion Estimation Algo-rithm. Proceedings of International Conference on Communi-cation Technology 2,2000:1173~1179
3 Y. Naito, T. Miyazaki, I. Kuroda. A Fast Full-Search Motion Estimation Method for Programmable Processors with a Multiply-Accumulator. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, 1996:3221~3224
4 Uwe Meyer-Baese, Digital Signal Processing with Field Pro-grammable Gate Arrays,2001
5 张益贞,刘 滔.Visual C++实现MPEG/JPEG编解码技术.北京:人民邮电出版社, 2002