近年来，随着计算机和网络技术的迅速发展，越来越多的社会团体、机关、企事业单位建立了计算机网络，人们更多的将社会活动、办公以及科研等各个方面活动的重心转移到了网络当中，形成了由局域网络为节点组成的庞大的互联网络。在互联网络节点之间越来越多的数据交换任务需要完成，以实现计算机软、硬件资源和信息资源的共享。在互联网络这种开放系统中进行数据交换，对于安全级别要求较高的数据，传输过程中的数据安全是至关重要的。
    网络数据传输安全的核心是通过对数据发送、网络传输、数据接收各个环节中的数据进行加密处理，以达到实现数据安全的目的。保护在公用网络信息系统中传输、交换和存储的数据的保密性、完整性、真实性、可靠性、可用性和不可抵赖性等。而加密技术则是数据传输安全的核心。它通过加密算法将数据从明文加密为密文并进行通信，密文即使被黑客截取也很难被破译，然后通过对应解码技术解码密文还原明文。
    目前国际上通用的加密方法主要有对称加密和不对称加密，不同的加密方法有不同的特点，在数据传输高安全性要求比较高的网络系统中得到了普遍采用，例如电子商务、邮件传输等方面。

1 加密算法的现状
    密码学是为了保证在发送者和接收者之间传递的数据不被第三者获得而对要传递的数据进行加密使其获得保密的科学。通常将传递的数据称为明文，为了保护明文，以将其通过某种方式变换成无法识别的密文，这个变换过程称为加密；另一方面密文可以通过相应的逆变换再还原成明文，这个过程称为解密。
    加密算法可以看作是一个复杂的函数变换：
    C=F(M，Key)
    式中：C代表密文，即加密后得到的字符序列；M代表明文，即待加密的字符序列；Key表示密钥，是秘密选定的一个字符序列。
    当加密完成后，可以将密文通过不安全渠道送给数据接收人，只有拥有解密密钥的数据接收人才可以对密文进行解密，即反变换得到明文。密钥的传递必须通过安全渠道。
    目前通用的加密算法主要分为对称和非对称算法。对称算法采用相同的密钥进行加密和解密。常用的对称加密算法有AES、IDEA、RC2／RC4、DES 等，其最大的困难是密钥分发问题，必须通过当面或在公共传送系统中使用安全的方法交换密钥。对称加密由于加密速度快、硬件容易实现、安全强度高，因此仍被广泛用来加密各种信息。但对称加密也存在着固有的缺点：密钥更换困难，经常使用同一密钥进行数据加密，给攻击者提供了攻击密钥的信息和时间。非对称算法，采用公钥进行加密而利用私钥进行解密。公钥是可以公开的，任何人都可以获得，数据发送人用公钥将数据加密后再传给数据接收人，接收人用自己的私钥解密。非对称加密的安全性主要依赖难解的数学问题，密钥的长度比对称加密大得多，因此加密效率较低，主要使用在身份认证、数字签名等领域。非对称加密的加密速度慢，对于大量数据的加密传输是不适合的。非对称加密算法包括RSA、DH、EC、DSS等。目前比较流行的、最有名的非对称加密算法是RSA。
    RSA的安全性在于大整数因子分解的难度，其体制构造是基于数论的欧拉定理，产生公开密钥和秘密密钥的方法为：
    (1)取2个互异的大素数p和q；
    (2)计算n=p×q；
    (3)随机选取整数e，且e与(p-1)×(q-1)互为素数；
    (4)另找一个数d，使其满足(e×d)mod[(p-1)×(q-1)]=1；(n，e)即为公钥；(n，d)为私钥。对于明文M，用公钥(n，e)加密可得到密文C，C=Me mod n；对于密文C，用私钥(n，d)解密可得到明文M，M=Cd mod n。
    利用当今可预测的计算能力，在十进制下，分解2个250位质数的积要用数十万年的时间，并且质数用尽或2台计算机偶然使用相同质数的概率小到可以被忽略。由此可见，企图利用公钥和密文推断出明文或者企图利用公钥推断出私钥的难度极其巨大，几乎是不可行的。因此，这种机制为信息传输提供了很高的安全保障。
    由上述内容可以发现，无论是对称加密和非对称加密的过程都是完成如下的过程：
    (1)产生密钥key；
    (2)C=F(M，Key)，即使用已经产生的密钥，通过加密算法将明文转换为密文。
    (3)数据传输；
    (4)M=F’(C，key)，即接收方使用解密算法，将密文转换为明文。
    如果需要传输的明文数据庞大，则加密和解密的算法的耗时将非常长，并且数据传输时也会占用大量的网络资源。也就是以上的(2)，(3)，(4)三个过程都会占用大量的时间和资源，如果能够降低这3个过程的时间，就会节省大量的资源，提高数据传输的效率。通过使用哈夫曼编码对文件进行压缩，就可以大大降低以上3个环节的处理时间，并同时在传输处理过程中减少计算机资源和网络资源的占用。

2 哈夫曼编码介绍
    哈夫曼编码是20世纪50年代由哈夫曼教授研制开发的，它借助了数据结构当中的树型结构，在哈夫曼算法的支持下构造出一棵最优二叉树，把这类树命名为哈夫曼树。因此，准确地说，哈夫曼编码是在哈夫曼树的基础之上构造出来的一种编码形式，它的本身有着非常广泛的应用。
2．1 基本原理
    数据能够被压缩的理论依据如下：
    定义1  对于给定的信源和码符号集，若有一个惟一可译码，其平均码长L小于所有其他惟一可译码，则称这种码为紧致码或最佳码。
    定理1  哈夫曼编码是紧致码。
    计算机文件是以字节为单位组成的，每个字节的取值为O～255。每个字节都看成字符，共256种字符。因此，每个字节都是以8个二进制位的定长编码表示的。由于这种定长码也是惟一可译码，根据定理1有L≤8。
    设某个文件有N个字节组成，则该文件总长度为8N比特。如果对该文件进行哈夫曼编码，则该文件总长度为LN比特。由于L≤8，所以LN≤8。所以，只要文件满足L<8，用哈夫曼编码总可以对其压缩。
    哈夫曼编码是一种变长编码，即通过使用较短的码字来给出现概率较高的信源符号编码，而出现概率较小的信源符号用较长的码字来编码，从而使平均码长最短，达到最佳编码的目的。由于哈夫曼编码只能对概率已知的信源符号编码，因此是一种统计编码。
2．2 构造哈夫曼编码表
    获得一个文件的哈夫曼编码表是该文件获得压缩与解压的关键。设某个文件中含有q种字符S1，S2，…，Sq，并且统计出每种字符在文件中出现的概率分别为p(S1)，p(S2)，…，p(Sq)，则编码的具体方法如下：
    (1)将q个信源符号按概率大小递减排列p(S1)≥p(S2)≥…≥p(Sq)；
    (2)用字符‘O’和‘1’分别代表概率最小的2个信源符号，并将这2个概率最小的信源符号合并成1个信源符号，从而得到只包含q-1个符号的新信源，称为缩减信源S1；
    (3)把缩减信源S1的符号仍按概率大小递减次序排列，再将其最后两个概率最小的信源符号分别用字符‘O’和‘1’表示，并且合并成一个符号，这样又形成了q-2个信源符号的缩减信源S2；
    (4)依次继续下去，直至信源最后只剩下两个信源符号为止，将这最后两个信源符号分别用字符‘O’和‘1’表示；
    (5)然后从最后一级缩减信源开始，进行回推就得到每种字符所对应的由字符‘O’和‘1’组成的字符串序列，不妨将其称为伪码字。
    这样，就为需要压缩的文件建立了一个一一映射f：Si→ci=1，2，…，q。式中：Si代表不同的字符，ci代表对应字符Si的伪码字。
    为了将伪码字变成真正的码字，又必须建立一个映射g：ci→ω，i=1，2，…，q。式中：ci代表不同的字符，(ωi代表对应字符ci的码字。该映射g 的功能是将由字符串组成的伪码字变成二进制数，比如g(010110)=(010110)2=(22)10。从而g[f(Si)]，i=1，2，…，q，就是构造的哈夫曼编码表。
2．3 文件压缩过程
    每从文件中读出一个字符char，用查哈夫曼编码表的方式得到对应的码字，然后用这个码字替换相应的字符g[f(char)]。当文件中的所有字符都经过了码字替换，则得到一个比原文件要小的压缩文件。文件之所以能够被压缩，是因为每个字符都占8个二进制位的空间。然而，通过码字替换相应的字符后，有的码字比相应的字符的码长要短，有的码字比相应的字符的码长要长，但文件在被压缩后总的长度比原来要短。
2．4 文件解压过程
    文件的解压过程是文件的压缩过程的逆过程，即将一个压缩文件还原成它的本来面目。因为一个压缩文件是不能够直接使用的，只有被解压后才能使用。一个被压缩的文件如果不能被解压，则这种压缩是毫无意义的。
    哈夫曼编码是即时码，只要得到码字c，则经查哈夫曼编码表得到相应字符f-1(g-1(c))，用这个字符替换相应的码字就是还原的过程。因此，每从压缩文件中读出一个码字，就从哈夫曼编码表查得相应的字符替换，当文件中所有的码字被替换掉，这个解压过程也就完成了。

3 高效网络安全传输方法设计
    一个高效的数据传输系统必须保证数据在传输中的安全和可靠，包括信息的保密性、完整性，同时在实现数据传输中占用更少的资源。所以数据加密传输的方案中应包括对发送端数据的有效加密、密钥的分配、传输数据的压缩。下面主要从信息的压缩、保密性几个方面来考虑数据加密传输系统中的加密方案。
    从哈夫曼编码压缩的过程可以看出，经过该方法压缩的数据必须使用压缩形成的哈夫曼编码树才能解压缩。对于不同的源文件，由于文件内容的不同，形成的哈夫曼编码树不同。数据传输的过程中需要同时传输压缩数据包和相应的哈夫曼编码树结构。相对于压缩数据包，哈夫曼编码树的节点数大大小于数据文件的数据量，如果只对哈夫曼编码树进行加密，加密和解密需要处理的数据量将大大减少，对于不对称加密算法无法处理大量数据的限制也可被克服。在数据传输中需要传输的数据量比压缩之前需要传输的数据量大大降低，可以节省大量的网络资源。在大规模的数据安全传输中，可以提高数据传输的效率和安全性。
    在信息的保密性方面选择RSA作为哈夫曼编码加密传输系统中传输信息的加密算法，采用公钥加密来发送哈夫曼编码。
    具体的数据传输实现的框架如图1所示。


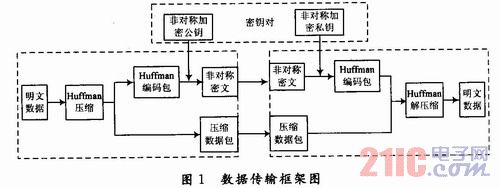
    安全数据传输的各个模块的功能如下：
    对需要传输的明文数据进行哈夫曼压缩，压缩完成后产生哈夫曼编码树的代码集合；用哈夫曼代码集合对原明文代码集合进行压缩转换；对哈夫曼代码集合进行RSA算法的公钥加密；传输加密后的哈夫曼代码集合和压缩代码集合；接收端收到数据后，使用私钥解密哈夫曼
代码集合；使用哈夫曼代码集合接压缩形成解压文件。

4 结语
    在数据安全传输过程中，通过对哈夫曼压缩后的明文数据进行改进的加密，克服了非对称加密算法加密大数据量文件的缺点，保持了非对称加密的安全性。通过压缩减少了数据传输的数据量，节省了网络带宽的开销，提高了数据传输的效率。这种方法非常适合大量的数据进行互联网络安全传输。此种方法只有在明文文件中数据的种类及出现的概率都完全相同的极端情况下，数据的传输效率才会降到最低。