1引言

在DC/DC" title="DC/DC">DC/DC变换器" title="变换器">变换器中，电压反馈控制" title="反馈控制">反馈控制因具有设计分析较简单、低阻抗功率输出、负载调整率较好等优点,而被广泛应用于DC/DC变换器中。其缺点是任何输入电压" title="输入电压">输入电压或输出负载的变化必须首先转化为输出电压的变化，然后再经反馈环采样控制调节，这意味着动态反应速度慢。输入电压变化带来的问题，一般可采用电压前馈技术解决。而要获得系统的快速性，主要有以下方案可供选择： 1）引入电流负反馈；

2）在主电路中增加阻尼极点或补偿极点；

3）提高开关频率以减小低通滤波器电感或电容

值；

4）采用PID调节。

其中唯有4）采用PID调节是较为可行的方法[1]。但单纯的PID调节对于处理DC/DC变换器的非线性等问题不够理想。模糊控制正好可以弥补这方面的不足。

近年来，随着芯片技术的不断发展，特别是DSP芯片价格的下降和速度的提高，DC/DC变换器控制技术正向着数字化、智能化控制方向发展。这是开关稳压电源高精度控制发展的必然趋势，也是21世纪开关稳压电源研究的一个重要课题。

考虑到以上各种因素，本文以Buck电路为例，介绍电压反馈控制模式下,DC/DC变换器系统数字模糊PID控制的原理、方法与实现。

2Buck电路动态小信号分析

考虑实际电感和电容存在电阻值，设分别为RL、RC(如图1所示)。根据状态空间平均法，可得到Buck电路的状态平均方程为：=AX＋BUin（1）

Uout=CX（2）式中：X=；

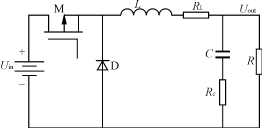
图1   Buck变换器电路拓扑图

图2Buck变换器开环控制方框图

(b)PID控制系统" title="控制系统">控制系统的频率特性

图3系统开环及使用PID控制的频率特性BODE图

A=；B=；C=；

Uin为输入直流电压；

Uout为输出电压。引入小信号变量：x=X＋，uin=Uin＋，及d=D＋代入式（1）得：=A＋B＋E（3）式中：E=；

D为占空比。

式（3）即为Buck电路动态小信号状态平均方程,将式（3）转换到s域并解之，可得到电压反馈控制下动态小信号模型的传递函数" title="传递函数">传递函数：=（4）

3模糊PID控制实现由式（4）可知，电压反馈控制为二阶系统，而二阶系统是一个有条件的稳定系统，只有对控制电路进行精心设计和计算，满足一定条件，才能使闭环系统稳定工作。考虑到输入电压变化量和占空比变化量(s)均对输出有影响，变换器系统的开环控制框图如图2所示。

图中N(s)为变换器输出对d(s)而言的系统开环传递函数，G1(s)可由（4）得出：G1(s)=

在电压负反馈控制中，如果引入输入电压前馈校正控制环，就能消除输入电压波动对系统的干扰，进而很好地改善系统的控制性能。为进一步提高控制性能与精度，控制电路采用具有微分和积分控制作用的数字PID控制。PID控制器中微分控制能预测事物的变化趋势，可以补偿由低通滤波器引起的时间滞后；积分控制能消除系统静态误差。从而采用PID控制，能增加系统的快速性和有效抑制超调，使系统动态性能和控制精度得以改善。由系统的BODE图（图3）可以看

(a)开环系统的频率特性

()开关电源

(a)系统输入电压阶跃变化(b)受扰动电压负反馈控制波动图

(c)受扰动PID控制波动图(d)受扰动模糊PID控制波动图

图6仿真结果

Buck变换器的数字模糊PID控制

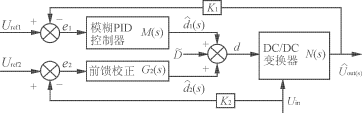
图4Buck变换器模糊PID闭环控制框图

图5Buck变换器模糊PID控制框图

出，系统开环的频率特性较差，采用PID控制后，不仅改善了系统的相角裕度，同时也降低了系统在低频时的增益。应用模糊控制对PID参数Kp、Ki、Kd实时地进行整定，则能改善PID的控制性能、自调整能力，从而可提高整个系统的控制精度和抗干扰能力。

3.1控制电路设计系统的闭环控制框图如图4所示。取输出电压的误差和微分量，送入模糊控制器和PID控制器，由模糊控制器根据输入控制量偏差实时给出PID的参数，再由PID控制器给出控制信号，从而实现对变换器的精确控制。取输入电压的误差送入系统前馈校正电路中，输出补偿量加入到模糊PID控制输出量，和一起组成变换器的占空比控制量d。图中：Uref2、Uref1分别为输入和输出参考电压；采用上一周期的输出占空比值，而不用静态值D，这样可确保系统的平滑性和稳定性；M(s)为模糊PID控制器的传递函数；G2(s)为前馈补偿函数。

3.2PID参数的整定

对于线性系统，PID参数的整定方法有多种，如：

1）ZieglerNichols频率响应法[2]；

2）Cohencoon响应曲线法[3]；

3）基于积分平方准则ISE整定法[4]；

4）极点配置法；

5)根轨迹法；

6)工程整定法等等。

实际上，DC/DC变换器为一非线性系统，而PID控制只适用于线性系统或有限范围波动的非线性系统，用一组事先整定好的PID参数，难以达到很好的控制效果，故其适用范围有限。为提高PID控制系统的控制性能和适用范围，必须根据偏差实时地改变Kp、Ki、Kd这三个参数，即实时调节PID控制器的增益。其控制框图如图5所示。

首先可由DC/DC变换器静态模型，依据上述线性PID参数整定法，得到较优的Kp，Ki和Kd静态PID参数值。模糊控制器依据偏差对应每一量化等级，都可得到相对应范围内较优的Kp′，Ki′和Kd′瞬时值。

一般来说Kp′在偏差e绝对值较小时取较小值，反之取较大值，这样有利于加快响应速度，同时保证有很好的稳定性；Ki′在偏差e绝对值较小时取较大值，反之取较小值，这样既有利于保证稳态无静差，又不会引起积分饱和而使超调增大、调节时间延长；微分系数Kd′在偏差e的绝对值较小时取较大值，反之取较小值，这样有利于加快对小偏差的反应速度，提高控制器对干扰的灵敏度，在出现干扰时可及时调节。

4仿真及实验结果

本控制系统实验采用TMS320F240型DSP，输入交流电压为110～250V，输出为直流10V，频率为60kHz，L=120μH，C=960μF,带电阻性负载。应用PSPICE对本系统进行了仿真，仿真结果如下图6所示。实验结果如图7所示，在t=0.035s时，系统受到输入电压的阶跃干扰。由仿真和试验结果可知，模糊PID控制具有较满意的控制效果和较快的动态性能。 5结语

本文通过状态平均法，获得了Buck电路电压反馈控制下的动态小信号模型和传递函数，其控制系统采用数字模糊PID控制。通过使用对非线性、时滞系统具有较好控制效果的模糊控制，对PID参数进行监控，大大提高了PID控制系统的精度、响应速度和适用范围。仿真与实验结果表明，采用本控制方法，系统具有较高的电压调整精度和较快的动态响应速度，适用范围大，抗干扰能力强等特点，特别是抗输入电压干扰能力。由于采用数字控制，控制系统可调整性好，抗外界干扰能力也得到加强。另外，如果本控制方法与遗传算法相结合，利用遗传算法进行对模糊规则的设计和控制，则可弥补模糊控制器缺乏系统设计方法的缺点，从而实现对变换器的智能控制[5]。