引言

不论是传统工艺制作的经典传感器，还是半导体工艺制作的现代传感器，都存在交叉敏感。交叉敏感是引起单传感器系统不稳定的主要因素，表现为传感器标称的目标参量恒定不变，而其它非目标参量变化时，该传感器的输出值发生变化。几乎所有的传感器都存在对温度的交叉敏感且不仅仅是一个交叉敏感量。以压力传感器为例，其标称的目标参量——压力恒定，而传感器的环境温度T或供电电压U/电流I变化时，其输出电压值发生变化，表明压力传感器存在对环境温度T及供电电压U/电流I两个非目标参量的交叉敏感。存在交叉敏感的传感器系统性能不稳定，准确性差，为了解决这一问题，可采用多传感器模型法技术来改善传感器系统性能。其基本思路是：当主测参量为x1的传感器存在干扰量x2时，若欲消除干扰量x2的影响，则需监测该干扰参量x2，从而建立测量x1与x2的多(2个)传感器系统；若欲消除n个干扰量的影响，则需测量n+1个参量的多(n+1个)传感器系统。

人工神经网络具有较强的非线性映射能力、较好的学习和容错能力，在函数逼近、预测、信号处理、控制系统领域中得到广泛的应用。径向基(RBF)神经网络是一种典型的性能良好的三层前馈局部人工神经网络，具有较快的训练速度和非线性能力，能以任意精度全局逼迫一个非线性函数，使其在很多领域得到广泛应用。本文采用RBF神经网络，监测干扰量温度T的温度传感器的输出电压为UT，监测干扰量恒流源供电电流I的电流传感器的输出电压UI，改善压阻式压力传感器(JCY-201)的温度稳定性与恒流源供电电流的稳定性，构建的三传感器数据融合智能系统框图如图1所示。

图1 三传感器数据融合智能系统框图

径向基(RBF)神经网络

径向基神经网络包含三层，即输入层、径向基隐层和线性层。

RBF神经网络模型

RBF神经网络的神经元作用函数采用高斯型函数，高斯型函数的数学表达式如式1：

式1

高斯函数的输出为1和0.5所对应的输入之间的差值称为函数的分散度(spread)，明显地，对应于式1的分散度为0.833。

RBF网络的神经元的总输入是权值矩阵的行向量与输入向量的向量距与偏置值的乘积，其数学表达式为式2：

式2

其中：ni为网络隐层第i个神经元的总输入；bi为第i个神经元的偏置值； 为隐层权值矩阵的第i个行向量的第j个元素；pji是第i个输入向量的j时刻输入值。

RBF神经网络的输出层通常是纯线性神经元，只是其隐层神经元是称之为radbas型的神经元。RBF神经网络模型如图2所示。

图2 径向基神经网络模型

RBF神经网络训练

由高斯函数的表达式可知，其输出最大值为1，当输入向量与权值向量的向量距减小时，神经元的输出增大。偏置b用来调节高斯函数对输入的灵敏度，b的绝对值越大，神经元对输入越灵敏，也就是说，神经元的响应函数曲线越“宽”，即高斯函数的输出为0.5时的两个总输入之差的绝对值最大。对于b的取值，一般由训练样本的样本距和样本的范围决定，b的取值大于两个相邻样本点的最大距离，而小于任意两个样本的最大距离。例如，对于一个单输入单输出的RBF神经网络，输入的样本为{-6,-4,0,2,4,7}，那么b的取值应大于4而小于13。

表1 学习样本的各物理量取值

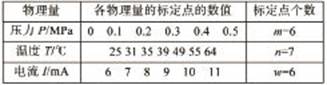
表2 检验样本的各物理量取值

RBF神经网络中，其隐层神经元的数量可以说是由样本点的数量来决定的，有多少个输入样本，就有多少个隐层神经元。对于每个隐层神经元的输入，其输出满足下列条件：（1）若是其对应的样本点，我们也称其为该神经元的特征输入点，那么其对应的输出应趋于1；（2）对于非样本点输入，输入与特征输入的点距离越远，则神经元的输出越小。因此，RBF神经网络的输入权值是由样本决定的，而与期望输出并没有太大关系。

在输入权值、隐层神经元的偏置b全部确定好之后，隐层的输出也就确定了。由于RBF神经网络的输出层神经元的响应函数是纯线性函数，因此，在选定输出层神经元之后，隐层与输出层之间的神经元连接权值可以由式3确定：

其中： 为输出层第i个神经元与隐层第j个神经元的连接权值；bi为输出层第i个神经元的偏置值；aj为隐层第j个神经元的输出向量；T为理想输出矩阵。求解式3，即可得到输出层与隐层的连接权值。

三维标定实验

为了训练RBF神经网络，确定网络的各权值和偏置的具体数值，使得网络的输出值与标定值之间能够达到误差精度的要求且具有一定的推广能力，各标定点的数量应能满足神经网络训练的要求。为了全量程范围内全面检验融合后稳定性的改善效果，实际上共标定个标定点，选其中7组不同温度的标定点（共252组数据）作为神经网络的学习（训练）样本，其余的3组不同温度的标定点（共108组数据）作为网络的检验样本。

学习样本各标定点的具体数值见表3。

表3 RBF神经网络用JCY-201型压力传感器三维标定实验数据——学习样本

检验样本各标定点的具体数值见表4。

表4 RBF神经网络用JCY-201型压力传感器 三维标定实验数据——检验样本

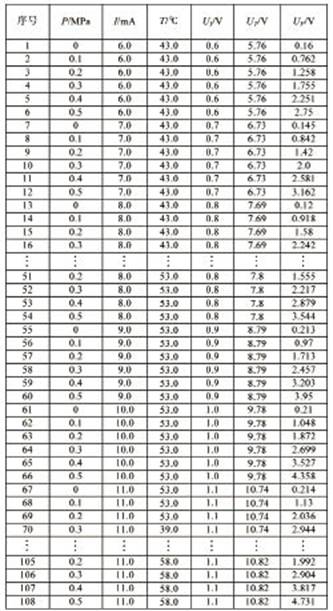
注：UI为电流传感器输出电压，UT为温度传感器输出电压，UP为压力传感器输出电压，表4同。

RBF神经网络Matlab源程序

RBF神经网络Matlab源程序如下：

clc

clear

close all %程序开始前，清屏，清除其它变量

%输入原始数据，每一列为一个变量，行数为样本的个数。原始标定数据的输入，可以将数据直接输入至程序中，也可以将数据先输入至文件，然后在程序中读入数据文件。数据中的P、Ut、Ui、Up均为维列向量， 为标定数据点的个数

raw_data=[P Ut Ui Up]； %学习（训练）样本

data_test=[P_test Ut_test Ui_test Up_test]； %测试样本

%根据原始数据制作学习（训练）样本与测试样本，学习样本与测试样本的数据格式相同

P=raw_data(: , 1); Ui=raw_data(: , 2); Ut=raw_data(: , 3); Up=raw_data(: , 4);

P_test=data_test(: , 1); Ui=data_test(: , 2); Ut=data_test(: , 3); Up=data_test(: , 4);

P1= ; [Up Ui Ut] %学习样本输入

T1= ; P' %学习样本期望输出

P2= ;[Up_test Ui _test Ut_t est]' %测试样本输入

T2=P_test' ； %测试样本输出

%将输入数据进行归一化

[PN1，Minp，maxp，TN1，mint，maxt]=premnmx(P1，T1)；

PN2=tramnmx(P2，minp，maxp)；

TN2=tramnmx(T2,mint,maxt);

%训练

switch 2

case 1 %神经元数是训练样本个数

spread=0.1； %此值越大，覆盖的函数数值就越大（默认为1）

net=newrbe(PN1，TN1，spread)；

case 2 %神经元数逐步增加，最多就是训练样本个数

goal=1e－8； %训练误差的平方和（默认为0）

spread=0.1； %此值越大，需要的神经元就越少（默认为1）

MN=size(PN1,2)； %最大神经元数（默认为训练样本个数）

DF=2； %显示间隔（默认为25）

net=newrb(PN1，TN1，goal，spread，MN，DF);

case 3

spread=0.1； %此值越大，需要的神经元就越少（默认为1）

net=newgrnn(PN1，TN1，spread);

end

%测试

YN1=sim(net，PN1)； %学习（训练）样本实际输出

YN2=sim(net，PN2)； %测试样本实际输出

MSE1=mean((TN1－YN1).ˆ2 %学习（训练）样本实际输出的均方误差

%n1=length(TN1)；%e1=sum((TN1－YN1).ˆ2/n1

%e1与MSE1相等

MSETD1=std((TN1－YN1).ˆ2

MSE2=mean((TN2－YN2).ˆ2 %测试样本实际输出均方误差

%n2=length(TN2)；%e2=sum((TN2－YN2).ˆ2/n2

%e2与MSE2相等

MSETD2=std((TN2－YN2).ˆ2

%反归一化

Y1=postmnmx (YN1,mint,maxt)' %将归一化的学习（训练）输出数据恢复为原始数据

E1=Y1－P %学习（训练）输出数据与标定值之间的偏差

Y2=postmnmx (YN2,mint,maxt)' %将归一化的测试输出数据恢复为原始数据

E2=Y2－P_test %测试输出数据与标定值之间的偏差

max(E2)

min(E2)

采用经过数据归一化处理的程序

神经网络采用Matlab中的newrb()函数，neurons=252。学习样本经RBF神经网络训练后的输出值与相应的压力标定值之间的最大误差绝对值为1.0396e－011，均方误差MSE1=5.6613e－023，均方误差的标准差MSETD1=2.4666e－022。这里省略学习样本的预测输出表。可见，采用RBF神经网络对学习样本的输出已经消除了压力传感器的交叉敏感影响（在误差允许的范围内）。

检验样本经RBF神经网络的输出值与相应的压力标定值之间最大偏差绝对值为max=0.0113，均方误差MSE2=3.8568e－005，均方误差的标准差MSETD2=2.1727e－004。输出样本的详细情况见表5（只列出部分数据）。

数据融合效果评价

降低温度与电源波动两个干扰量的影响，传感器系统稳定性的改善程度分别用融合前后的零位、灵敏度温度系数以及电流影响系数来评价。

由于学习（训练）样本的网络输出值与标定值之间的偏差很小（均小于1.0e－011），如果根据这些数据来计算融合后的效果，可以认为已经完全消除交叉敏感。通过表5可知，本例中检验样本的网络输出值与标定值之间的偏差与学习样本的偏差相比，偏差较大，故按检验样本计算出数值来评价数据融合效果。

表5 输出样本

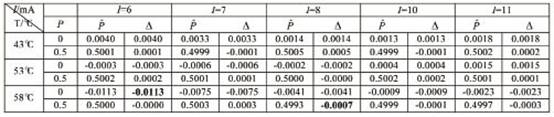
注：表中T表示工作温度，I表示工作电流，P表示压力标定值，表示压力计算值，偏差，单位都是V。

融合前：满量程输出值UFS=4.928V，当温度的变化范围为=39℃（由25℃至64℃），电流由6mA至11mA，变动时，零点值的最大变化范围=0.356V（由0.328V至-0.028V），满量程输出值由4.928V下降到2.710V，输出变化范围=-2.218V。

（1）零位温度系数

（2）灵敏度温度系数

（3）电流影响系数

利用检验样本计算的融合后的零位温度系数、灵敏度温度系数以及电流影响系数如下：

在=39℃，变化范围内，零点融合计算值的最大偏差 =0.0113MPa；满量程压力PFS=0.5MPa，其融合计算值的最大偏差量=0.0007MPa，则有

将融合前和RBF神经网络融合后的各参数列于表6中。

表6 融合前和RBF神经网络融合后的各参数

从表6可见，经RBF神经网络融合后，零位温度系数降低到融合前的1/3，灵敏度温度系数降低约3个数量级，电流影响系数降低约2个数量级

结束语

由于半导体的特性参数易受温度、电流的影响而变化，压阻式传感器将会产生很大的零位温度漂移、灵敏度温度漂移和电流影响漂移，这是压阻式传感器最大的弱点。因此，研究改善压阻式压力传感器的温度稳定性与恒流源供电电流的稳定性，在生产实践中很有意义。采用RBF神经网络法，设计了抗两个干扰量影响的智能化软件模块，对压阻式压力传感器稳定性进行改善，取得了很好的效果。该方法简单易行，精度较高，将压阻式压力传感器输出精度控制在0.01%以内。