摘  要： 有限脉冲响应(FIR)数字滤波器的设计，实质上是一个多参数优化问题。将粒子群优化算法与混沌相结合来设计FIR数字滤波器，并用该方法设计了一个高通滤波器。与用Parks-McClellan算法设计得到的高通滤波器进行对比发现，基于混沌粒子群优化算法(CPSO)的FIR滤波器通带波动小，阻带衰减大，从而证明了该算法的有效性和优越性。
关键词： 混沌粒子群优化算法；FIR数字滤波器；滤波器设计

    FIR数字滤波器在满足一定对称条件下，可以实现线性相位，而且其结构中只用到前向路径，从而使其具有固有的稳定性，因此在通信、雷达、声纳、生物医学、地震勘探等领域得到了广泛的应用。传统的FIR数字滤波器设计方法有频率抽样法、窗函数法和一致逼近法。频率抽样法和窗函数法简单易行，但不易精确地确定其通带和阻带边界频率。一致逼近法[1]以Parks-McClellan算法为代表，该方法能获得较好的通带和阻带性能，并能准确地指定通带和阻带的边缘，是一种有效的设计方法。很多学者在FIR数字滤波器设计问题上做了大量的探索研究，并提出了用优化算法来设计FIR数字滤波器，它是在一定的优化准则下，使设计的滤波器性能最优。其中雷米兹(Remez)交换算法是最标准的优化算法[2]，但它对设计指标不仅有频域上的要求，而且又有时间响应的约束时，该算法就不再使用。采用加权最小二乘(WLS)设计算法虽然容易实现，但需要计算高阶矩阵的逆，当滤波器阶数很高时，这个矩阵的求逆将出现困难[3]。遗传算法是一种全局最优方法，但是遗传算法采 用了选择、交叉和变异等操作，算法结构复杂、运算量大、收敛速度慢[4-5]。
    粒子群优化算法PSO(Particle Swarm Optimization)[6]是由EBERHART和KENNEDY博士在1995年提出的一种新的全局优化进化算法。该算法源于对鸟群捕食行为的模拟，算法的突出特点是结构简单，运行速度快，计算量小、程序实现非常简洁，需要调整的参数少。但在实际应用中，PSO也表现出了易产生早熟收敛、局部寻优能力差等不尽如人意的问题。而混沌粒子群优化[7]可利用混沌变量的随机性、遍历性及规律性进行优化搜索，加快进化速度，改善粒子群优化摆脱局部极值点的能力。
    本文将混沌搜索机制与粒子群优化算法相结合，以克服PSO陷入早熟、局部寻优能力差的缺陷，并将其运用于FIR数字滤波器的设计。与参考文献[8]相比，本文算法的混沌搜索策略是初始化产生混沌粒子，然后把混沌变量从混沌空间映射到解空间，利用混沌变量进行搜索。
1  混沌粒子群优化算法设计FIR数字滤波器



    通过这样的改进，w在算法初期较大，算法搜索的空间也就较大；w在算法晚期很小，可以提高算法的精细搜索能力。
    混沌粒子群算法(CPSO)通过将混沌搜索机制有机地引入粒子群优化算法，使每个粒子从混沌搜索机制与粒子群算法搜索机制中获得适当的搜索方法，以混沌变量的遍历性增强粒子的搜索性能与更全面应用目标函数的信息，并反映到逐代更新的个体极值和群体极值中，可更有效地调整粒子的移向并最终获得最优解。
    混沌优化算法的基本思想是初始化产生混沌粒子，然后把混沌变量从混沌空间映射到解空间，利用混沌变量具有遍历性和随机性的特点进行搜索。

    采用自适应惯性权重的混沌粒子群优化算法设计FIR数字滤波器的具体实现步骤如下：
   
   图1为CPSO和标准PSO两种粒子群优化算法寻优得到的群体最优解进化曲线。由图可知，相比于标准PSO算法，CPSO算法寻优得到的均方误差更小，且与参考文献[9]中最大迭代次数设定为2 000相比，混沌粒子群优化算法在迭代次数小于1 000时，就可以收敛到最优值， CPSO算法耗时更少。

    图2为CPSO算法寻优得到的FIR数字滤波器的脉冲响应。

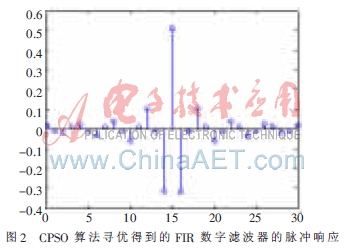
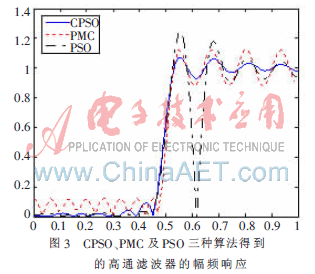
    图3是CPSO、PMC及PSO三种算法得到的高通滤波器的幅频响应，实线为CPSO算法得到的曲线，点划线为PSO算法得到的曲线，虚线为Parks-McClellan算法得到的曲线。由图可以看出：CPSO算法得到的滤波器比PSO算法得到的滤波器的通带更平稳，比Parks-McClellan算法得到的滤波器的通带波动更小，阻带衰减更大。

    本文用混沌粒子群优化算法得到滤波器系数，进而设计FIR数字滤波器。通过对一个实例的设计，可以看出，混沌粒子群优化算法设计得到的滤波器，与Parks-McClellan算法设计的滤波器相比，滤波器性能更优良。但是，粒子群优化算法的研究和应用尚处于初级阶段，很多方面还有待进一步的探索研究，如算法的收敛性、参数选取等问题，以及如何与其他方法更好地结合，以达到更好的寻优效果。
参考文献：
[1] 胡广书.数字信号处理—理论算法与实现[M].北京：清华大学出版社，1997.
[2] 程佩青.数字信号处理教程[M].北京：清华大学出版社，1995.
[3] LEE J H， CHEN C K， LIM Y C. Design of discrete coefficient FIR digital filters with arbitrary amplitute and phase responses[J]. IEEE Transactions on Circuits and Systems， 1993， 40：444-448.
[4] 杨福宝.基于遗传算法的FIR数字滤波器的优化设计[J].武汉理工大学学报(交通科学与工程版)，2002，26(4)：478-480.
[5] 郑力新，周凯汀，王永初.基于遗传算法和窗函数的FIR滤波器新设计方法[J].电子测量与仪器学报，2002，16(1)：49-53.
[6] KENNEDY J， EBERHART R C. Particle swarm optimization[C]. IEEE International Conference on Netural Networks. Perth， Australia， 1995， 11(27)： 1942-1948.
[7] 杨俊杰，周建中，喻菁，等.基于混沌搜索的粒子群优化算法[J].计算机工程与应用，2005(16)：69-71.
[8] 杨延西，刘丁，辛菁.基于混沌粒子群优化的图像相关匹配算法研究[J].电子与信息学报，2008，30(3)：529-533.
[9] SHI Y， EBERHART R C. A modified swarm optimizer[C]. IEEE International Conference on Evolutionary Computation.Anchorage， AK USA， 1998：69-73.
[10] 周飞红，刘辉，廖子贞.粒子群优化算法在FIR数字滤波器设计中的应用[J].计算机工程与应用，2008，44(33)：83-85.