摘 要: 在借鉴传统PID控制应用于单片机的方法的基础上,引进了模糊规则的调用方式。根据偏差绝对值和偏差变化绝对值的改变,调节PID参数,最后进行Matlab仿真。经过对没有加入PID控制、加入传统PID控制与加入模糊PID动态性能的差异比较,验证被控系统的动态性能得到明显的改善。
关键词: 模糊PID;传统PID;Matlab仿真
传统PID(比例、积分和微分)控制原理简单,使用方便,适应性强,可以广泛应用于各种工业过程控制领域。但是PID控制器也存在参数调节需要一定过程、最优参数选取比较麻烦的缺点。对一些系统参数变化的过程,PID控制就无法有效地进行在线控制,不能满足在系统参数发生变化时PID参数随之发生相应改变的要求,严重影响了控制效果[1]。本文介绍了基于给定系统的模糊PID控制,它不需要被控对象的数学模型,能够在线自动根据参数的变化实时修正参数,使控制器适应被控对象参数的任何变化,并对其进行仿真验证。
1 传统PID与模糊PID的比较
1.1 PID控制
PID控制器问世至今凭借其结构简单、稳定性好、工作可靠、调整方便等优点成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握、得不到精确的数学模型时,采用PID控制技术最为方便。PID控制器的参数整定是控制系统设计的核心,它根据被控过程的特性来确定PID控制器的参数大小。PID控制原理简单、易于实现、适用面广,但PID控制器的参数整定是一件非常令人头痛的事。合理的PID参数通常由经验丰富的技术人员在线整定,在控制对象有很大的时变性和非线性的情况下,一组整定好的PID参数远远不能满足系统的要求。为此,本文引入了一套模糊PID控制算法。
1.2 模糊PID控制
所谓模糊PID控制器,即利用模糊逻辑算法并根据一定的模糊规则对PID控制的比例、积分、微分系数进行实时优化,以达到较为理想的控制效果。模糊PID控制共包括参数模糊化、模糊规则推理、参数解模糊、PID控制器等几个重要组成部分。计算机根据所设定的输入和反馈信号,计算实际位置和理论位置的偏差e以及当前的偏差变化ec,并根据模糊规则进行模糊推理,最后对模糊参数进行解模糊,输出PID控制器的比例、积分、微分系数[2]。
2 给定被控系统
2.1 被控系统的组成
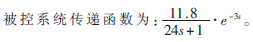
系统由两部分组成:惯性环节和时间延迟环节组成,如图1所示。

2.2 模糊PID控制器的设计
PID参数的模糊自整定是找出PID三个参数Kp、Ki、Kd与e和ec之间的模糊关系,在运行中通过不断地监测e和ec,并根据模糊控制原理对三个参数进行在线的整定。
PID参数的设定依靠经验及工艺的熟悉,参考测量值与设定值曲线,从而调整Kp、Ki和Kd的大小。在此系统自动采用如下公式对Kp、Ki、Kd参数进行调整:
Kp=kp0+#kp
Ki=ki0+#ki
Kd=kd0+#kd
其中#kp、#ki、#kd是模糊控制器的输出量,kp0、ki0、kd0是由系统参数整定出来的,在此使用了如下整定公式:
kp=[(0.703+0.530 7×T÷L)×(T+0.5L)]÷[K×(T+L)]
Ti=T+0.5L
Td=0.5×L×T÷(T+0.5×L)
最终得到被控系统的初始PID参数是:
kp0=0.398 259,ki0=0.0 156 157,kd0=0.562 248。
这个初始参数的合理给定对整个模糊控制系统造成很大的影响。在此处使用的参数整定方法经最终的实验得知是非常合适的。
模糊控制规则是用于修正PID参数的,模糊控制规则根据过程的阶跃响应情况来考虑求取。规则如表1所示。
根据上述模糊控制规则,采用如下的PID参数的调节规则,如表2、表3、表4所示,其中每个表格的第一行表示误差变化量ec的模糊集合,第一列表示误差e的模糊集合。

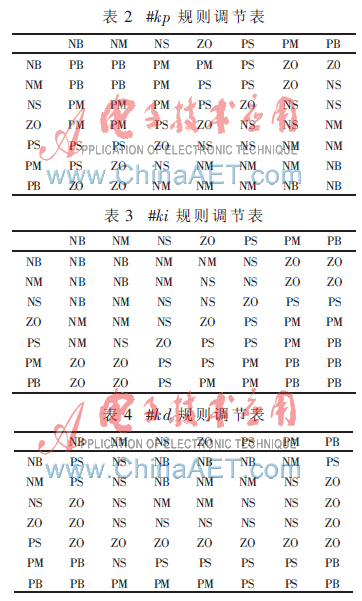
PID三个参数的模糊规则库建立好以后,就可以根据模糊控制理论进行参数的自调整。将系统误差e,误差变化量ec,#kp、#ki、#kd的变化范围定义为模糊上的论域:e,ec={-3,-2,-1,0,1,2,3},#kp={-0.3,-0.2,-0.1,0,0.1,0.2,0.3},#ki={-0.06,-0.04,-0.02,0,0.02,0.04,0.06},#kd={-3,-2,-1,0,1,2,3}。
在模糊控制规律中,e、ec、#kp、#ki、#kd的语言变量值取“负大”(NB)、“负中”(NM)、“负小”(NS)、“零”(ZO)、“正小”(PS)、“正中”(PM)、“正大”(PB)共7个值。它们的隶属度函数都是三角形,并且每个值所取的范围宽度相等。
3 仿真
3.1 仿真程序
本模糊控制器仿真程序是以m文件的形式给出的,需要运行时,只要把此m文件程序放到Matlab软件中直接运行即可,不需要其他任何操作[3]。
3.2 仿真结果
为了验证PID模糊控制器的控制效果,用Matlab/Simulink软件进行仿真,根据系统的数学模型,仿真框图如图2所示。
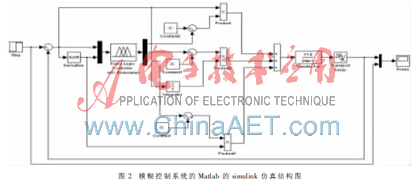
运行仿真程序,得到如图3所示的仿真结果。从图中可以知道,在阶跃响应下,图4所示的没有过程控制PID仿真与图5所示的传统过程控制PID仿真相比,该系统的上升时间稍有改进,调节时间大大缩小,超调量明显减小,大大提高了系统的动态性能,由此可以明显看出本文设计的模糊PID控制系统具有明显的优越性。
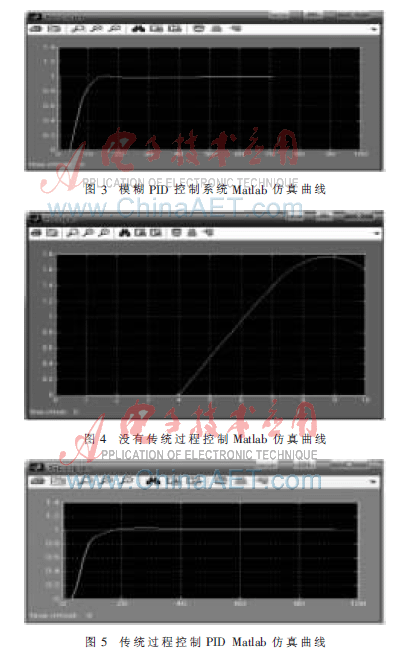
从图3的最终仿真图中,可以明显地看出加入PID控制器后给整个系统的响应带来极大的改善,同时还可以看出模糊控制器在控制系统中所起的作用,因为在传统过程 PID控制系统已经取得很好的控制效果的前提条件下,正是由于模糊控制器的引入使得整个控制系统的控制效果又取得了更大更好的进展,具体表现在被控系统的上升时间进一步减小,但还是没有满足最初对于系统的性能要求,这也是本系统设计的一个不足之处,是需要继续改进的地方;系统超调量进一步减小,从而完全满足了对于被控系统的要求;5%稳定时间进一步地满足系统的性能要求;系统稳态误差最终是0,完全满足系统性能要求;系统阻尼程度进一步减小。
本论文将模糊控制与Simulink相结合,对给定被控系统设计了一个比较合理的模糊PID控制器并且进行Matlab仿真。由于被控系统处于一个实时变化的环境,系统参数可能会根据环境变化。传统的固定控制参数的控制策略没有办法满足这样的需求,而模糊自适应控制却恰好弥补了这一缺陷。同时模糊自适应控制还很好地解决了系统本身自带的由于惯量引起的误差。本文的创新点是结合给定被控系统分析设计了模糊PID控制器,并进一步给出了自适应模糊推理与优化方案,现场实验效果良好。还需要改进的地方主要表现在:(1)在本文中系统响应的上升时间始终没有小于10 s,需对系统继续改进;(2)当被控系统接入斜坡信号时,对没有过程控制PID的控制系统与具有传统过程控制PID的控制系统,相比较后者的效果明显好于前者,但是当本文设计的模糊PID控制系统接入斜坡信号时,其输出却是发散的情况,需对系统继续改进。
参考文献
[1] 韩力群.智能控制理论及应用[M].北京:机械工业出版社,2008.
[2] 爱民.模糊控制技术[M].西安:西安电子科技大学出版社,2008.
[3] 黄忠霖,黄京.控制系统Matlab计算及仿真[M].北京:国防工业出版社,2009.

