摘  要： 介绍了基于递推最小二乘法进行系统辨识的基本原理，对给定的实际输入输出数据运用MATLAB的M语言编写递推最小二乘算法，最后给出相应的仿真结果和分析，并对得到的模型进行验证。
关键词： 系统辨识；递推最小二乘；MATLAB；仿真

    对于一个系统，在输入输出数据的基础上，从一组给定模型类中，确定一个与所测系统等价的模型，这种方法叫做辨识。辨识是在实际应用中获取系统模型的最为重要的手段之一，也是数学模型和实际应用联系的纽带。而最小二乘类辨识则是在给定的结构框架下，利用模型输出与实际输出间的误差不断纠正模型参数，最终得到最优模型的过程[1]。在使用最小二乘法进行参数估计时，为了实现实时控制，必须优化成递推算法RLS（Recursive Least Square），主要用于在线辨识。MATLAB是一种面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言（如C、Fortran）的编辑模式，代表了当今国际科学计算软件的先进水平[2]。
    本文使用MATLAB2009a的M语言对递推最小二乘算法进行编程，最后使用MATLAB自带的辨识工具箱SIT(System Identification Toolbox)对得到的仿真结果进行了验证。
1 线性系统辨识[3]
1.1 问题描述

其对应的辨识问题的表达形式如图2所示。
    图2中，h(k)和z(k)是模型的输入输出变量，在离散点上必须是可观测的；v(k)为模型噪声；?兹是未知模型参数。

2 仿真实例[4]
2.1 选择输入信号
    为了准确辨识系统参数，对输入信号有如下要求：在辨识时间内，过程的动态必须被输入信号持续激励。从谱分析角度看，这就意味着信号频带能覆盖系统的频带宽度。除此之外还要求信号有可重复性，不能是不可重复的随机噪声，因此本文选择满足上述要求的M序列作为输入信号。
2.2 先验知识
    在对给定的过程进行辨识之前，掌握如下先验知识：纯迟延d=0；模型如式(7)所示，且数据长度L=1 000，na=nb=4。

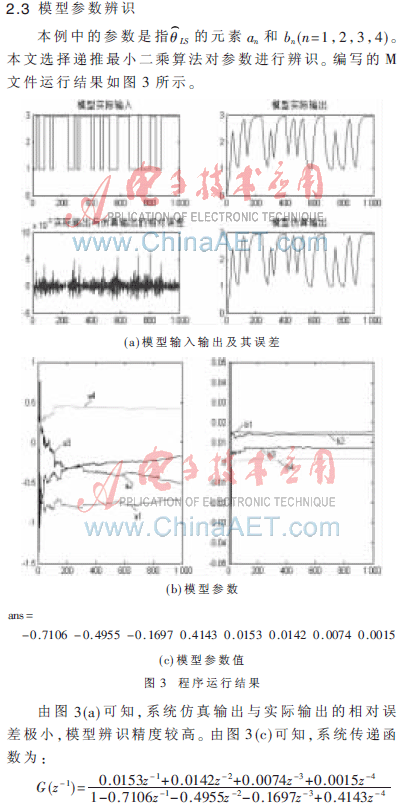
2.4 模型验证
    本文使用MATLAB自带的辨识工具箱SIT(System Identification Toolbox)对得到的仿真结果进行验证。在MATLAB2009a的Command Window中输入ident命令，SIT被打开。需将给定的输入输出数据设置为该模块的输入输出方可进行验证。结果如图4所示。

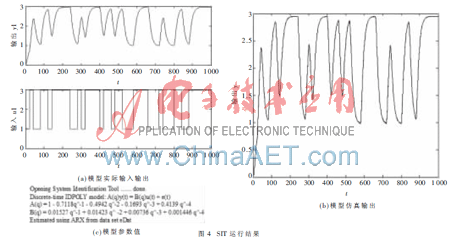
    由图3(c)和图4(c)中所得的模型参数可以看出，本文编写的递推最小二乘算法可以快速准确地估计出系统参数，获得较好的辨识结果。
    本文介绍了基于递推最小二乘法进行系统辨识的基本原理，对给定的实际输入输出数据运用MATLAB的M语言编写递推最小二乘算法，最后给出相应的仿真结果和分析，并对得到的模型进行了验证。递推最小二乘法的算法简单，能减少计算量，减少数据在计算机中占用的内存，并实时辨识出系统动态特性以供实时控制和预报。
参考文献
[1] 倪博溢，萧德云.MATLAB 环境下的系统辨识仿真工具箱[J].系统仿真学报，2006，18(6)：1493-1496.
[2] 石贤良，吴成富.基于MATLAB的最小二乘法参数辨识与仿真[J].微处理机，2005，26(6)：44-46.
[3] 方崇智，萧德云.过程辨识[M].北京：清华大学出版社，1988.
[4] 张志涌.精通MATLAB6.5版[M].北京：北京航空航天大学出版社，2003.