摘  要： 采用一种处理非平稳信号的新方法—希尔伯特-黄变换HHT（Hilbert-Huang Transform）来进行滚动轴承故障特征的提取。将信号先进行小波包降噪处理，然后用HHT进行信号故障特征提取。通过实验仿真和轴承故障诊断实例，对比没有进行小波包降噪而直接进行HHT的结果，证明了此方法在轴承故障诊断中的有效性。
关键词： 小波包降噪；Hilbert-Huang变换；EMD；IMF；滚动轴承

　滚动轴承是机械设备最为关键部件之一，其损伤将直接影响设备稳定运行，因此轴承故障的分析与诊断一直是机械故障诊断技术中的重要内容。由于轴承信号一般表现为非平稳、非线性，且易受随机噪声干扰，难以有效提取故障特征。Hilbert-Huang变换[1]是一种新的信号分析方法，被认为是近年来对以傅里叶变换为基础的线性和稳态谱分析的重大突破，具有很高的应用价值。
1 小波包降噪
　小波包变换是在小波变换的基础上发展起来的，具有比小波变换更高的分辨率。小波包分析最基本的应用是信号的消噪，小波包降噪[2]的步骤为：
　（1）信号小波包分解。选择一个小波，确定其所需要分解的层次N。
　（2）计算最优树（即确定最优小波包基）。计算一个给定熵的标准最优树。
　（3）小波包分解系数的阈值量化。选择一个恰当的阈值，并对小波包分解系数进行阈值量化。
　（4）信号的小波包重构。
2 Hilbert-Huang变换
　Hilbert-Huang变换是HUANG N E提出的一种信号处理方法，是由EMD和Hilbert分析组成[1]。
2.1 EMD
　EMD方法通过对非平稳信号中不同尺度的波动或趋势逐级分解，来获得一系列表征信号特征时间尺度的固有模态函数IMF（Intrinsic Mode Functions）。IMF满足两个条件[3]：一是在整个序列中，极值点与过零点个数必须相当或相差不到一个；二是任何一个时间点上，信号局部极大值组成的上包络线和下包络线的均值为零。经验模态分解[4]步骤如下：
　（1）把原始信号作为待处理信号，确定该信号所有局部极值点，通过插值将全部极大值点和极小值点连接起来得到信号的上、下包络线，取包络线均值m（t），从待处理信号x（t）中减去均值，得：
h1（t）=x（t）-m（t）（1）
通常h1（t）一般不满足IMF的定义，需重复上述步骤k次，直到h1k（t）是IMF，记c1（t）=h1k（t）为信号第一个IMF，也是最高频率分量。

　对比两图，可看到小波包能够除去信号中噪声的影响，而HHT具有良好的时频分析能力。
4 滚动轴承故障诊断实例分析
　在电动机的滚动轴承实验台上测量振动加速度信号。

　在时域波形图中，正常轴承和内圈、滚动体故障时域图基本相同，而外圈故障表现为频繁的冲击成分。在频域波形图中，正常轴承频率主要在低频段，而故障频率信息较为复杂，如外圈故障频率在整个频率段内都有分布等，故无法根据时、频域波形图进行故障分析。
　采用本文中EMD方法，以轴承外圈故障为例，获得EMD分解如图5所示。图5（a）故障信号分解为12个模式，c1~c11是IMF分量，分别为不同频率分量段，第12个是残余分量。图5（b）经小波包降噪后信号分解为10个模式，可见小波包能很好地去除频率的虚假成分，减少分解层次，使IMF分量更为集中在不同频段。

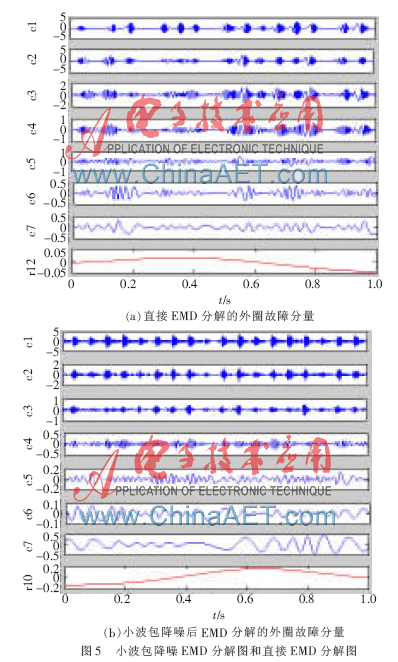
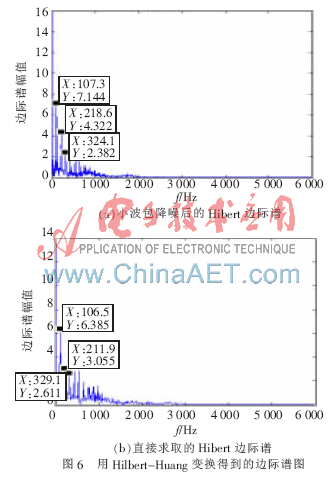
　图6所示为边际谱图，图6（a）的第一个故障频率为107.3 Hz，而图6（b）为106.5 Hz，其余为其倍频，对比外圈故障的特征频率理论值，可知用小波降噪后的HHT方法，能够较为准确地反映外圈故障时的特征频率。

　本文通过Hilbert-Huang变换的方法，结合小波包的信号降噪处理能力，先对信号进行降噪处理，使信号得到更有效的分解模式；然后再由HHT获得其边际谱，来提取滚动轴承的故障频率。通过以上实验仿真及轴承故障实例分析，证明了小波包降噪和HHT的方法在滚动轴承的故障诊断中的可行性。
参考文献
[1] HUANG N E， SHEN Z， LONGS R， et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proc. R. Soc. Lond，1998，454： 903-995.
[2] 曾宪伟，赵卫明，许晓庆.基于小波变换与小波包变换的降噪方法比较[J].地震地磁观测与研究，2010，31（4）：14-19.
[3] 张仕海，等.EMD中异常事件处理及其在转子动平衡中的应用[J].振动与冲击，2012，31（7）：34-38.
[4] 徐美娟.基于EMD的Hilbert变换在齿轮检测中的应用[J].机电信息，2012（3）：107-108.