文献标识码: A
文章编号: 0258-7998(2015)02-0059-02
0 引言
FIR滤波器具有严格的线性相频特性,同时又可保证任意幅频特性。而这个特点使FIR滤波器在数据传输、图像处理和识别、语音处理和通信系统中具有广泛的应用。除此之外,FIR滤波器除0以外没有其他的极点,所以整个滤波系统是相对稳定的,不存在不稳定的问题,这是FIR区别于IIR的本质原因,而FIR在传输数据时存在色散。
本文只讨论FIR滤波器的设计方法。基于DA算法的滤波器有效解决了MAC结构的不足,但是随着滤波器的阶数增加,查找表的规模呈指数增加,再设计高阶滤波器时普通DA算法甚至难以实现。本文提出了一种优化的DA算法来克服一般DA算法在设计高阶滤波器时的缺陷,并用Verilog HDL语言在FPGA上实现[1]。
1 线性相位FIR滤波器的结构
如果FIR中的h(n)为实数,并符合下列条件其中的一种:
偶对称:h(n)=h(N-1-n)
奇对称:h(n)=-h(N-1-n)
称其具有线性相位结构。
当N为奇数时,其系统函数为[2]:
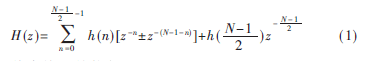
其直接型结构如图1所示。

当N为偶数时,其系统函数为:
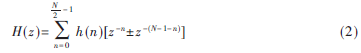
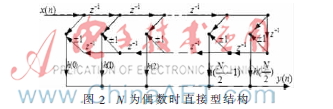
其直接型结构如图2所示。
2 分布式算法
2.1 分布式算法基础
DA算法是基于查找表结构的,其详细公式解析如下[3]:

重新分配求和的顺序,其结果如下:
y=c[0]( xB-1[0]2B-1+ xB-2[0]2B-2+…+ x0[0]20)
+c[1]( xB-1[1]2B-1+ xB-2[1]2B-2+…+ x0[1]20)+…
+c[N-1](xB-1[N-1]2B-1+xB-2[N-1]2B-2+…+x0[N-1]20)
=(c[0] xB-1[0]+c[1] xB-1[1]+…+c[N-1]xB-1[N-1])2B-1
+c[0] xB-2[0]+c[1] xB-2[1]+…+c[N-1]xB-2[N-1])2B-2
+…+(c[0] x0[0]+c[1] x0[1]+…+c[N-1] x0[N-1])20
(6)
2.2 分布式算法的优化
假如N的数量增加,一个单一的LUT无法执行全字,就能够利用部分表并先将结果相加。其原理为:假定长度为LN的内积 ,那么可以用一个DA体系结构实现它:
,那么可以用一个DA体系结构实现它:
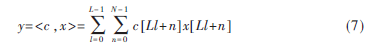
表的规模从一个24N B的LUT减少4个2N B表。优化的DA算法的结构图如图3所示。
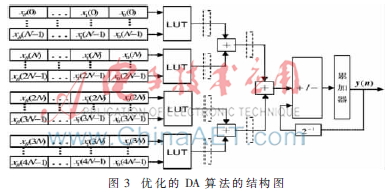
3 基于FPGA的FIR低通滤波器的设计
3.1 基于FPGA的FIR设计流程
本文设计的FIR滤波器的流程如图4所示,主要分为系数提取和FPGA完成[4]。
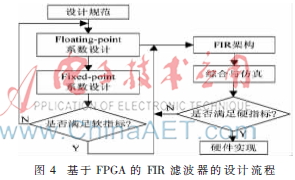
3.2 FIR滤波器的MATLAB设计
本文设计滤波器主要参数为阻带最小衰减为30 dB,通带波纹小于0.5 dB,截止频率为0.4。为此设计了18阶的FIR线性相位低通滤波器,采用窗函数中的凯泽窗来设计。根据凯泽窗参数?对滤波器的性能的影响,来满足条件。由这些技术指标可通过MATLAB提供的滤波器设计工具箱FDAtool来仿真设计滤波器,从而提取滤波器的系数[5]。
由于提取出来的系数是浮点型,而FPGA只能处理定点型数据,所以需要把提取出来的系数进行量化,在该设计方案中将系数扩大1 024倍,即210。再通过编码转化为二进制形式。通过FDAtool工具提取出的数据及其量化结果如下:
h(0)=h(17)=-0.014 361 548 558 709 025,
h(1)=h(16)
=0.000 000 000 000 000 007 952 163 344 493 980 7,
h(2)=h(15)=0.028 618 979 697 780 135,
h(3)=h(14)=0.024 250 698 402 580 449,
h(4)=h(13)=-0.033 323 873 349 896 04,
h(5)=h(12)= -0.075 849 033 020 568 446,
h(6)=h(11)
=0.000 000 000 000 000 014 598 689 803 221 391,
h(7)=h(10)=0.197 209 967 107 277 67,
h(8)=h(9)=0.373 454 809 721 535 27。
其量化结果分别为:-15,0,29,25,-34,-78,0,202,
382。十六进制补码分别为fff1,0000,001d,0019,ffde,ffb2,0000,00ca,017e。
3.3 线性相位FIR滤波器的FPGA实现
本文采用模块化思想,由一个主时钟控制各个子时钟,全部模块分别为并串转换、延时与预求和、移位累加、查找表采用3个分割查表结构和求部分和的模块[6]。
为了验证电路能否连续正确运行,本文连续随机输入序列0、127、100、57、26、5、20、26、79、8、12、49、35、102、99、125、63、82在Modelsim工具上进行仿真,其结果如图5所示。
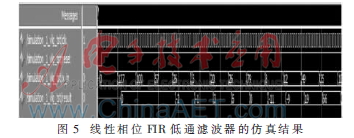
仿真结果与MATLAB工具计算的理论值相比较,其Modelsim部分仿真结果如下:0、-2、-1、3、6、0、-11、-9、
19、19、66。MATLAB理论计算结果对应为:0、-1.823 9、-1.436 2、2.816 0、5.568 3、-0.247 6、-11.1261、-9.084 2、
19.414 9、66.125 3。通过仿真与MATLAB计算理论结果进行比较,理论值与仿真结果存在误差但是误差在允许的范围内,误差主要是因为量化时产生的。
4 结束语
本文提出的优化DA算法本质是提出对查找表的优化,事实证明滤波器阶数越高,此优化算法的作用越明显,而且可以节省内部逻辑资源。最后通过硬件实现,结果与理论值相比较,设计符合预期。
参考文献
[1] 程佩青.数字信号处理[M].北京:清华大学出版社,2001.
[2] Meyer-Baese U(美).数字信号处理的FPGA实现[M].北京:清华大学出版社,2011.
[3] 杜勇.数字滤波器的MATLAB与FPGA实现[M].北京:电子工业出版社,2012.
[4] 高耀红.基于FPGA的FIR低通滤波器[D].长沙:湖南大学,2012.
[5] 刘朋全.基于FPGA的FIR数字滤波器的设计和实现[D].西安:西北工业大学,2006.
[6] 夏宇闻.数字系统设计教程[M].北京:北京航空航天大学出版社,2008.

