摘  要： 传统的OD矩阵估计方法大部分都是基于路段流量的，由于路段流量数目远小于OD对的个数，因而限制了这些方法的推算精度。针对拥堵路网，提出了一种基于路段转向流量的OD估计方法，以提高OD估计的精度。分析了路段转向流量能够降低OD的可行解集的范围。通过双层规划模型求解拥挤路网上OD估计问题。由于最大熵模型不依赖于先验OD矩阵，可以应用到更多的OD估计场景中，因此上层模型采用的是最大熵模型，下层采用用户均衡模型。实验结果表明：基于路段转向流量可以增加估计的精度。

　　关键词： OD矩阵估计；路段转向流量；最大熵模型；用户均衡模型；双层规划模型

0 引言

　　OD矩阵（Origin-Destination matrix），描述了一段时间内交通网络的所有起点到终点的交通出行量，反映了交通出行者对交通网络的基本需求。OD矩阵是城市交通规划、控制、交通流预测和智能交通系统[1]等的重要基础数据。而获取OD矩阵的传统方法需要非常大的时间成本和经济成本。一种替代的方法就是通过更易获取的路段流量和相关信息等来估计OD矩阵。

　　近几十年，已经有许多模型被开发出来用于OD估计，如最大熵模型[2]、广义最小二乘模型[3]、贝叶斯统计推断模型[4]和极大似然模型[5]等。上述的几种模型都将交通分配矩阵作为常量处理，即交通出行者的路径选择行为与OD矩阵无关，这种方法只适合拥挤效应不明显的路网，一般是交通量较小的路网。而在实际情况中，许多路网都是拥挤路网。拥挤路网的交通分配模型更加接近于用户均衡模型（UE）[6]，交通出行者的路径选择受OD矩阵的影响，即不同的OD矩阵会产生不同的交通分配矩阵。YANG H提出了将OD估计和交通分配过程进行综合考虑的双层规划模型[7]。在双层规划模型中，交通分配矩阵由模型本身确定，不是给定的常量，非常适合拥挤路网的OD估计问题。以上方法均是基于路段流量，通常情况下，由于路段流量的个数远小于OD对个数，OD矩阵可行解集较大，限制了OD估计的精度。于凯在最大熵模型中引入路段转向流量[8]，增加了模型的估计精度，但是模型基于不变的分配矩阵，不适用于拥挤网络。

　　近年来，一些新的观测手段用于OD估计，比如手机信息、GPS信息，这些信息可以增加OD估计的精度，但是不易获取而限制了其应用。通过传统方法进行OD估计仍然为目前的主要方法，本文基于易于获得的路段转向流量，提出了一种基于路段转向流量的OD估计双层规划模型。仿真实验表明：该方法可以提高拥挤路网OD估计的精度。

1 基于路段转向流量的OD估计模型

　　1.1 OD估计基本原理

　　交通网络可以用一个有向图G（V，E）表示，V为所有路段的集合，E为所有节点的集合。假设交通网络有m个路段观测流量，n个待估计的OD对，则基于路段流量的OD估计的基本方程组如下：

　　r=pq（1）

　　r=[r1r2…ri…rm]T，为路段观测流量向量；

　　q=[q1q2…qi…qn]T，是待估计的OD矩阵的向量形式；

　　p是m×n的交通分配矩阵，描述了路段流量r和OD向量q的线性关系；

　　p=[p1Tp2T…piT…pmT]T，其中（pi）1×n表示了第i个路段流量ri与q的线性关系。

　　OD估计问题就是在已知r和p的情况下求解方程组（1）的解q，通常情况下由于m<<n，q有无穷多解。为了求得唯一的q，可以引入一些模型将OD估计变为一个数学规划问题，形式如下：

　　min f（r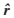，，q0，q）

　　s.t. r=pq（2）

　　q≥0

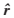　　：OD估计时求得的路段流量；

　　q0：先验OD矩阵。

　　1.2 引入路段转向流量的基本方程组

　　设第i个路段有si个转向，ri1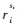，…，分别表示第1个，…，第si个转向流量。根据路段流量守恒有：

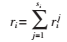　　（3）

　　第i个路段的第j个转向流量方程可以表示为：

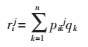　　（4）

　　pikj表示第k个OD量qk分配到i个路段的第j个转向流量rij的比例。

　　由式（4）易知同一个路段的流量方程与路段转向流量方程组线性相关，因此可以用路段i的转向流量方程组代替关于路段流量ri的方程，则可将式（1）的方程组改为：

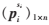　　表示了路段转向流量与q的线性关系。上面的方程组也可以表示为：

　　rl=plq（6）

　　rl表示既有路段流量，也有转向流量的向量；

　　pl矩阵表示rl与OD向量q的线性关系。

　　同理，其他有转向流量的路段都能引入到方程组r=pq中。实际上，一个路网的许多路段都能引入几个转向流量，使得方程组的个数增加，结果就是矩阵pl的秩增加，q解集的范围降低。

　　1.3 双层规划模型

　　双层规划模型的上层模型是最大熵模型EM，表示如下：

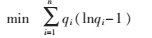
　　s.t. r=pq（7）

　　q≥0

　　已知r和p，模型EM可求得OD向量q。

　　分配矩阵p可以由下层模型（UE模型）解得。

　　其中，δis为1表示路径s经过路段i，否则为0；fi表示路径流量；W表示所有的路径集合；Wi表示OD对i之间的所有路径集合；ce（x）是路段旅行费用函数。

　　已知q，UE模型可以求得估计流量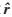，分配矩阵p。

　　引入部分路段上的转向流量后可以将上层规划模型EM中的等式约束改为rl=plq。

　　下层UE模型也可以求得估计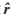，分配矩阵pl。

　　将基于路段流量的模型简述为BEMR，基于路段转向流量和路段流量的模型简述为BEML。

2 求解算法步骤

　　由于双层规划问题本身有非凸、非光滑的特性，求取最优解非常困难，大部分算法只能针对特定的模型给出近似解。本文给出的迭代求解方法可以求得近似较优解。单独求解上层最大熵问题（EM）和下层用户均衡分配问题（UE），目前都有比较有效的算法。并且引入了路段转向流量后，上层问题的搜索的可行解集的范围大大缩小，也使得求解这个双层规划问题的一个相对较优的解更加容易。

　　求解这类双层规划问题的有效算法是迭代优化算法。算法的主要思想就是先给出上层规划的初始决策变量，将这个决策变量传递到下层规划中，下层规划求解最优解，再将下层规划的最优决策传递到上层规划进行求解，如此反复求解上层规划和下层规划，最后双层规划问题的上层决策变量和下层决策变量趋于平稳，此时就是双层规划问题的相对较优的方案。根据这个方法，求解最大熵双层规划模型的思想是，先设定一个初始的OD矩阵求解下层的用户均衡交通分配问题，将下层规划求得的交通分配矩阵传递到上层最大熵模型中，并求解出最优的OD矩阵，最后模型趋于平稳，求得较优解。

　　用Q表示OD总量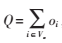，，Vo表示所有入口节点集合，oi表示O点的流量，通常情况oi都是很容易观测到的，所以可以将Q作为一个常量处理。因为没有先验OD矩阵，而通过分析入口处交通总量来获取初始迭代点是非常简单可行的，所以可以用交通总量的平均值作为初始点。

　　求解步骤如下：

　　（1）初始化qk=[q1k…qik…qnk]T，k=0，其中每个qik=Q/n。

　　（2）用qk求解下层规划问题，本文采用Frank-Wolfe算法求解，在这一步可以求得plk。

　　（3）用rl和plk求解上层规划问题来获取qk+1。设plk、rl分别是t×n的矩阵，t×1的向量（t>m），解决此问题，先引入拉格朗日乘数向量（λk）t×1，OD矩阵可以用拉格朗日乘数表示如下：

　　求解λk，将qk+1代入到（6）中有：

　　本文用Levenberg-Marquardt算法求解上述非线性方程组。求得λk，由式（9）就可以求得qk+1。

　　（4）检查终止准则，若不能终止则转步骤（2），并令k=k+1。终止准则由下式决定：

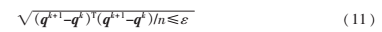
　　其中，ε为误差上限值。

3 仿真实验与分析

　　一个六路口的实验网络如图1所示，一共34个路段，90个OD对。除了10个出口路段，其他路段均有3个转向流量。基于路段流量的方程组总数为34个，基于路段流量和路段转向流量的方程组总数为24×3+10=82个，其中有部分方程是线性相关的。

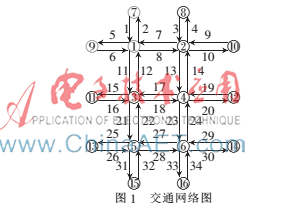
　　仿真实验中用一个真实的OD矩阵按照用户均衡模型分配到路网上，将分配所得的路段流量和路段转向流量作为OD估计的输入数据。根据估计所得的OD矩阵和真实的OD矩阵，比较BEMR模型和BEML模型的OD估计精度。

　　路段旅行费用函数采用BPR公式（Bureau of Public Road）：

　　ce（re）=ce（0）（1+0.15（re/Ce）4）（12）

　　Ce为道路通行能力；

　　ce（0）为平均自由流下的道路通行时间。

　　下面的统计参数可以表示OD估计的精度：均方根误差rmse，相对均方根误差trmse，相对平均值误差mae。

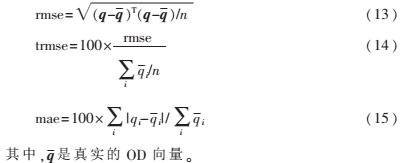
　　除此之外，还给出一个直观的指标?兹x，表示OD估计的结果中与真实OD相对误差小于等于x的OD对个数占总OD对个数的百分比。表示如下：

　　其中，card表示取集合元素总数。

　　表1为模型估计精度对比。从表1可以看出，基于路段流量和转向流量的模型各项统计指标均优于单纯基于路段流量的模型。当路网的路段流量和路段转向流量均可观测时，路段流量总约束条件为34个，而路段流量和转向流量的总约束条件为82个，显然后者包含的信息量更多，这使得OD估计的精度提高。

4 结论

　　采用基于转向流量的OD估计算法，能有效降低数学规划问题的可行解集的范围，提高了解的准确性。随着检测技术的进步，越来越多的城市能提供准确的转弯流量数据。实验结果表明：基于路段转向流量的OD估计的估计精度优于传统的基于路段的OD估计。

参考文献

　　[1] 丁革媛，李振江，郑宏云.智慧城市中的智能交通系统构建[J].微型机与应用，2013，32（24）：1-3.

　　[2] VAN ZUYLEN H J， WILLUMSEN L G. The most likely trip matrix estimated from traffic counts[J]. Transportation Research Part B： Methodological， 1980，14（3）：281-293.

　　[3] CASCETTA E. Estimation of trip matrices from traffic counts and survey data： a generalized least squares estimator[J]. Transportation Research Part B： Methodological， 1984，18（4）：289-299.

　　[4] MAHER N J. Inferences on trip matrices from observations on link volumes： a Bayesian statistical approach[J]. Transpor-tation Research Part B， 1983，17（6），435-447.

　　[5] SPIESSH. A maximum likelihood model for estimating origin-destination matrices[J]. Transportation Research Part B： Methodological， 1987，21（5）：395-412.

　　[6] SHEFFI Y. Urban transportation networks： equilibrium analysis with mathematical programming methods[M]. Englewood Ciiffs： Prentice-Hall Inc， 1985.

　　[7] YANG H， SASAKI T， IIDA Y， et al. Estimation of origin-destination matrices from link traffic counts on congested networks[J]. Transportation Research Part B， 1992， 26（6）， 417–434.

　　[8] 于凯.基于转弯流量的OD反推算法及基于微观对象的动态配流算法研究[D].杭州：浙江大学工业控制技术研究所，2006.