孔祥昆,于万波
(大连大学 信息学院,辽宁 大连 116622)
摘要:利用线性函数迭代系统进行迭代可以绘制出树与山等自然景物,而非线性系统在这方面的研究结果相对较少。本文利用辅助函数与一个随机生成的多项式函数构成动力系统,其中辅助函数具备类似正弦函数的性质,而多项式函数只含有二次项或者一次项,通过绘制分形图等方法对系统的混沌特性进行分析,结果表明,一组三维正弦函数与两个三维多项式函数构造的动力系统是混沌的概率很高,通过迭代可以得到众多的具有观赏和实用价值的三维吸引子。除了可以辅助绘制吸引子图形外,这种构造混沌的方法也是混沌理论研究的一个实例。
关键词:混沌;吸引子;曲面;迭代
0引言
近年来,研究人员对函数迭代系统(Iterated Function System)进行了深入的研究[1],取得了许多研究成果。例如,研究人员使用线性迭代系统绘制出树、山等自然景物,从而诞生了分形几何这一新的学科分支;在非线性函数迭代的研究方面得到了著名的Julia集合与Mandelbrot集合等研究成果[2]。此外还有M.F.Barnsley研究得出的拼贴定理[3]。在其他各个学科领域中,都有关于迭代系统的经典实例,例如,由简单多项式函数构成的描述大气运动的Lorenz系统[4],这一系统促使研究人员开始对混沌进行深入研究;化学反应中也有着许多混沌系统,如Brussels振子[5];一些人工神经网络中的系统等也可以出现混沌[6]。对于什么样的函数构成动力系统才可以出现混沌,文献[7]选择插值拟合曲面进行研究。文献[7]研究发现,如果式(1)

中的曲面f(x,y)是双二次有理贝塞尔(曲面)函数,而另外一个曲面g(x,y)是随机生成的多项式曲面,则式 (1)所示的动力系统出现混沌的概率可以大于十分之一。在此基础上,文献[89]研究了三角函数曲面与随机多项式曲面构成动力系统的混沌特性,发现在一定的参数区间内,出现混沌的概率可以超过90%,所以三角函数是一种(目前来看)最好的辅助函数。文献[9]使用三维辅助函数,例如三维三角函数、小波函数、Logistic函数等与两个三维随机多项式函数构成动力系统,研究发现其是否出现混沌与三维函数的截面形状有直接关系。
本文在以上研究基础上,进一步研究了什么样的曲面构成的动力系统是混沌的,以及如何使用迭代函数系统生成更多的图形图案,以用于工业设计、动漫设计等领域。
1二维正弦函数与随机多项式函数构成动力系统
作为辅助函数,正弦函数具有很好的特性,振荡并占有一定的空间,与另外一个二次随机多项式构成动力系统,如式(2)所示。使用该动力系统进行迭代,能够构造出大量的混沌系统[8]。
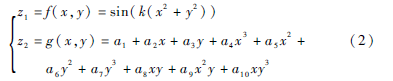
本文进一步研究发现,正弦函数与其他形式的随机多项式构成动力系统也可以很容易出现混沌,并且能够产生大量独特的吸引子图形。
1.1二维正弦函数与没有xy项的随机二次函数构成动力系统
式(2)中系数是随机生成的,其中某个系数为0的可能性比较小。如果令某些系数为0,则:

令式(3)中的k=3.141 59,随机生成g(x,y)表达式的系数,其为-1~1之间的数。为了确保迭代能够正常进行,将多项式g(x,y)函数值调整到-1~1之间。调整方法是:首先计算多项式函数在[0, 1]× [0, 1]区域上的最大值g(x,y)max和最小值g(x,y)min,然后使用式(4)进行调整:

调整之后的函数经过仿真模拟绘制出吸引子图形,如图1所示。

得到4个吸引子的系数a0,a1,a2,a3,a4分别为:
(a)0.401 3,0.965 4,0.613 3,0.407 1,-0.030 1;
(b)0.831 9,0.204 0,-0.492 9,0.746 9,0.026 8;
(c)0.656 1,0.835 1,-0.773 8,0.624 3,0.816 5;
(d)-0.086 1,0.576 3,-0.437 9,-0.550 4,0.817 7。
当式(3)中g(x,y)的常数项与一次项系数都为0时,如式(5)所示,这种情形下,也易于出现混沌,但是因为参数少,所以吸引子样式减少,很容易得到一些中间过渡的吸引子图形,如图2所示,其中f(x,y)的参数k=3.141 59。


系数分别为:(a)0.756 6,0.283 3;(b)0.369 3,0.957 0;(c)-0.812 1,0.300 1;(d)-0.990 6,0.206 2。
实验结果发现,当g(x,y)没有平方项或有xy项时,如式(6)与式(7),不易出现混沌。

当g(x,y)有常数项、一次项、平方项,也有立方项时,如式(8)所示,可以绘制出众多吸引子,如图3所示。
f(x,y)=sin(k(x2+y2))
g(x,y)=a0+a1x+a2y+a3x2+a4y2+a5x3+a6y3 (8)
得到的吸引子系数分别为:

(a)-0.120 2,0.866 8,0.366 7,0.678 5,0.257 6,-0.574 9,-0.732 5;
(b)-0.535 3,0.609 7,0.816 8,-0.521 4,-0.900 5,-0.536 2,-0.843 2;
(c)-0.248 2,-0.980 2,-0.160 3,0.587 7,0.839 9,0.507 3,0.689 4;
(d)0.867 7,-0.725 6,0.043 2,0.790 4。
由图3可知,当式(8)中g(x,y)=a0+a1x+a2y+a3x3时,出现混沌吸引子的概率小一些(大约在0.5),不过会出现一些面积比较大的混沌,如图2(d)所示。
为了提升出现混沌吸引子的概率,把式(8)中的f(x,y)调整为f(x,y)=sin(k1 x2 + k2 y2),就会很容易出现混沌,如图4所示。

此时,吸引子系数分别为:
(a)0.539 8,-0.249 9,0.646 8,-0.906 7,0.195 8,0.898 3,-0.422 4,k1=3.141 59,k2=3.8;
(b)0.332 2,-0.738 1,-0.809 2,-0.970 3,-0.423 6,0.633 5,0.971 0,k1=3.141 59,k2=2.8。
1.2二维正弦函数与随机多项式函数迭代出现混沌的条件分析
周期点在混沌研究中有着重要的作用。如果一个系统没有不动点(一周期点)和二周期点,那它就不是LiYorke混沌的,也不是Devaney混沌的。另外文献[8]分析了二维Devaney混沌产生的必要条件与周期点处的导数的乘积的绝对值之间的关系。
由文献[8]结论1和结论2可知,在构造混沌曲面迭代时,周期点处不能太平坦。这里所说的混沌需要满足Devaney混沌定义中的遍历性,即对定义域内任何两个开集U,V∈χ,存在自然数k。
结论1动力系统如式(1)所示,如果二元函数f(x,y)与g(x,y)定义域为[0,1]×[0,1],值域是[0,1],在定义域内存在关于x,y的偏导数。如果f(x,y)与g(x,y)构成的动力系统是混沌的,那么在其不动点(x0,y0)处存在关于x,y的偏导数,而且关于x,y的偏导数之和:|f′x(x0,y0)|+|f′y(x0,y0)|与|g′x(x0,y0)|+|g′y(x0,y0)|不能同时小于1。
结论2动力系统如式(1),如果二元函数f(x,y)与g(x,y)定义域为[0,1]×[0,1],值域是[0,1],在定义域内存在关于x,y的偏导数。f(x,y)与g(x,y)构成动力系统,如果在这个动力系统的两个周期点(x0,y0)与(x1,y1)处关于x,y的偏导数满足条件: |f′x(x0,y0)|+|f′y(x0,y0)|<1,|g′x(x0,y0)|+|g′y(x0,y0)|<1,|f′x(x1,y1)|+|f′y(x1,y1)|<1,|g′x(x1,y1)|+|g′y(x1,y1)|<1,那么该动力系统不是混沌的。
结论3二元连续可导函数构成动力系统如式(1)所示,如果对于N周期中的N个点(N为正整数),都满足式(9):

那么该动力系统不是混沌的。与Lyapunov指数相比,这种判断条件虽然不是充分条件,但是也能够排除诸多的非混沌系统,准确地验证一个系统是否是遍历混沌的。另外这种方法不需要计算特征值,不需要取对数,可以节省时间。
上面讨论的都是二维函数构成的动力系统,三维函数构成的动力系统也存在着类似于结论1和结论2的结果。
2多个动力系统构成非线性函数迭代系统
在第1节中研究的是二维函数构成动力系统的情形,下面将多个三维函数构成的动力系统组合在一起,构成随机非线性迭代系统,按照一定的概率,随机选取其中的某个动力系统进行迭代,这样,可以生成更多形式的更加复杂多样的吸引子图形。例如使用式(10)所示的动力系统构造随机非线性迭代系统:

使用4个如式(10)所示的动力系统组成一个迭代系统,当f(x,y,z)参数k分别取1.5、2、2.5、3,g(x,y,z)的系数如表1所示,h(x,y,z)的系数如表2所示,这时绘制出的吸引子图形如图5所示。
使用4个如式(10)所示的动力系统组成一个迭代系统,当f(x,y,z)参数k分别取1.5, 2, 2.5, 3;g(x,y,z)的系数如表3所示;h(x,y,z)的系数如表4所示,这时绘制出的吸引子图形如图6所示。
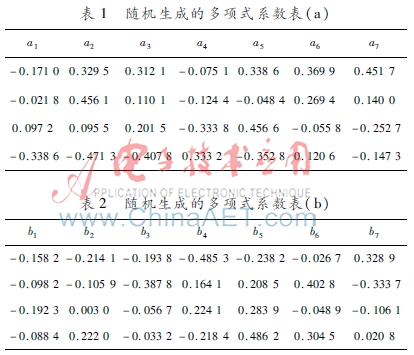

图6根据表3和表4系数绘制出的吸引子


3结论
本文给出了一种实用的混沌吸引子生成方法,利用正弦函数等混沌性质较好的函数与随机多项式函数构成动力系统进行迭代,可产生大量的具有观赏和使用价值的吸引子。图案几乎不可以穷尽,变化多端,有很多具有相当高的审美价值与研究价值。
使用少数的方程构成线性IFS迭代可以生成树、山等自然景物,使用非线性方程组进行迭代能否很容易地生成动物与人,这是一个需要进一步研究的工作。
参考文献
[1] DUMITRU D, LOANA L, SFETCU R C, et al.Topological version of generalized (infinite) iterated function systems[J] .Chaos,Solitons & Fractals, 2015(71):7890.
[2] AVERBECK N, RAINES B E. Distributional chaos in dendritic and circular Julia sets[J] .Journal of Mathematical Analysis and Applications,2015,8(15): 951958.
[3] Barnsley M F, HARRINGTON A N. A mandelbrot set for pairs of linear maps[J].Physica D: Nonlinear Phenomena, 1985,4(3):421432.
[4] Li Chunbiao, SPROTT J C, THIO W.Linearization of the Lorenz system[J].Physics Letters A, 2015, 5(10):888893.
[5] Zhou Changsong, Chen Tianlun. Chaotic neural networks and Chaotic annealing[J]. Neurocomputing, 2000,30(14):293300.
[6] 秦元勋,曾宪武.生物化学中的布鲁塞尔振子方程的定性研究[J].科学通报, 1980(8):337339.
[7] 于万波,周洋.空间单位区域双二次有理贝赛尔曲面混沌特性研究[J] .物理学报,2013(22): 2535.
[8] 于万波,赵斌.曲面迭代混沌特性研究[J].物理学报,2014(12):3141.
[9] 于万波.截面的几何形状决定三维函数的混沌特性[J] .物理学报,2014(12):2230.

