0 引言

    随着电子产业的蓬勃发展，BGA（Ball Grid Array）封装的芯片在航空航天设备中的应用越来越广泛，因此其使用过程中焊点的健康一直是人们关注的焦点^[1-4]。由于监测困难、监测周期长、一旦失效甚至有可能引发不可挽回的灾难性损失，所以对焊点的健康进行预测就显的尤为重要。

    概率统计、模糊数学和灰色系统理论是三种最常用的健康预测研究方法，其研究对象都具有某种不确定性。概率统计研究的是“随机不确定”现象，其出发点是大样本，并要求对象服从某种典型分布。模糊数学着重研究“认知不确定”问题，主要是凭经验借助于隶属函数进行处理。灰色系统理论着重研究概率统计、模糊数学所难以解决的“小样本”、“贫信息”等不确定性问题，因此适用于BGA焊点的健康预测。

1 灰色系统理论

    20世纪80年代初，华中理工大学邓聚龙教授提出灰色系统理论^[5-6]，该理论把随机过程看作灰色过程，认为任何随机过程都是在一定时间区域和幅值区域变化的灰色量，通过对原始数据的整理找到数据变化规律的过程。虽然采集到的数据没有表现出明显的规律性，而且数据样本较少，但这些数据蕴含着内在规律，利用该理论即可预测出某个时期内的规律，进而用来解决大量实际问题。差分、均值、离散1阶1变量灰色模型（GM(1，1)）是灰色系统理论的3种基本模型。

1.1 差分GM(1，1)模型

    假设通过实际测试采集到的原始数据序列为：

    称：

    式(3)为差分GM(1，1)模型。α为发展系数，代表的是行为序列估计值的发展态势；b为灰色作用量，是从行为序列中挖掘出来的数据，反映的是数据变化的关系。

1.2 均值GM(1，1)模型

    令：

    式(9)为均值GM(1，1)模型的白化微分方程，也叫影子方程。

1.3 离散GM(1，1)模型

    称：

    式(12)为离散GM(1，1)模型。

2 焊点健康预测

    焊点连接失效是在外界环境中各种应力的共同作用下，使得焊点逐渐老化、磨损，从而导致其性能下降，焊点的阻抗间歇性升高，随着应力的持续累积，单位时间内，其焊点阻抗间歇性升高的次数越来越多，直到最后完全失效。其变化过程是渐进性的而非突发性的，具有一定的规律性，因此可以运用灰色系统理论实现对焊点未来健康状态的预测，为焊点连接失效的健康管理提供依据。

2.1 数据采集

    利用已有监测手段，可以很容易得到两次焊点阻抗间歇性升高之间的间隔时间，以及每次焊点阻抗间歇性升高的持续时间，分别用Δt₁和Δt₂来表示。因为它们是环境应力累积下焊点连接老化的两种表现形式，所以Δt₁和Δt₂之间存在相关性，即Δt₁和Δt₂之间可以相互表示。对Δt₁和Δt₂的数据规律进行分析可知，在焊点健康状态退化的过程中Δt₁从大变小，而Δt₂则由小变大。对焊点健康状态的预测主要是在焊点连接退化的早期进行的，这时如果选择Δt₂，由于时间测量的不准确会导致预测精度的降低，故在用灰色模型对焊点连接失效进行预测时使用的数据源为Δt₁。

    文中采用的原始数据是故障诊断^[7]得到的实测数据Δt₁(t/min)，分别为：113.4、86.2、83.9、90.5、60.7、65.1、58.8、67.3、25.4、51.4、68、27.8、44.55、17.87、29.2、42.75、26.49、11.37、30.54、20.72、8.1、20.59。取前6次的数据用来建模及预测，其他实测数据用来与预测值进行对比分析。

2.2 模型建立

    由实测数据可得：

    X⁽⁰⁾={113.4，86.2，83.9，90.5，60.7，65.1}

    X⁽¹⁾={113.4，199.6，283.5，374.0，434.7，499.8}

    建立的3种模型如下：

    （1）差分模型

    x⁽⁰⁾(k)+0.113x⁽¹⁾(k)=119.144

    （2）均值模型

    （3）离散模型

    x⁽¹⁾(k+1)=0.919x⁽¹⁾(k)+99.995

2.3 软件仿真

    利用MATLAB软件和上面建立的模型，即可预测出两次焊点阻抗间隙性升高的累积时间，与实测值对比如下。

    （1）利用差分模型得到的预测值与实测值的对比情况如图1所示。

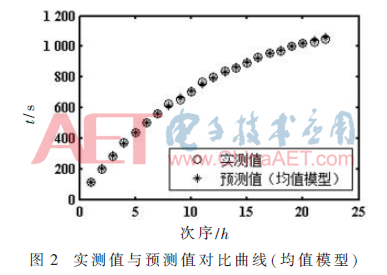
    （2）利用均值模型得到的预测值与实测值的对比情况如图2所示。

    （3）利用离散模型得到的预测值与实测值的对比情况如图3所示。

2.4 结果分析

    从仿真结果可以看出，利用灰色系统理论，针对BGA焊点，分别建立的差分、均值、离散GM(1，1)模型，都可以实现对其健康的预测，预测值与实测值基本吻合。通过对比3个图也可以看出，差分模型的预测值略大于实测值，离散模型的预测值略小于实测值，而均值模型的预测值与实测值吻合得较好。

3 结论

    （1）把灰色系统理论引入BGA焊点的健康预测，克服了概率统计、模糊数学难以解决的“小样本”、“贫信息”等困难。

    （2）利用灰色系统理论，分别建立了差分、均值、离散三种BGA焊点失效模型。

    （3）对比仿真结果，发现均值GM(1,1) 模型的预测值与实测值吻合得更好。

参考文献

[1] LIU C，WANG J Y，ZHANG A T.Research on the fault diagnosis technology of intermittent connection failure belonging to FPGA solder-joints in BGA package[J].Optik-International Journal for Light and Electron Optics，2013，125(2)：737-740.

[2] 陈颖，康锐.球栅阵列封装焊点寿命预测的综合方法[J].焊接学报，2009，30(11)：105-108.

[3] 田园，孙靖国，李大鹏.基于FPGA的BGA焊点健康管理原理与实现[J].计算机测量与控制，2015，23(10)：3310-3312.

[4] PERKINS A，SITARAMAN S K.Universal fatigue life prediction equation for ceramic ball grid array(CBGA) packages[J].Microelectronics Reliability，2007，47(12)：2260-2274.

[5] 邓聚龙.灰理论基础[M].武汉：华中理工大学出版社，2002.

[6] 刘思峰，杨英杰，吴利丰.灰色系统理论及其应用[M].北京：科学出版社，2014.

[7] 王建业，丁浩，刘苍.FPGA焊点连接失效故障诊断[J].焊接学报，2014，35(8)：66-70.