文献标识码: A
DOI:10.16157/j.issn.0258-7998.190962
中文引用格式: 武小超,陈鸿. 基于半边结构的STL文件快速拓扑算法[J].电子技术应用,2020,46(1):92-95,99.
英文引用格式: Wu Xiaochao,Chen Hong. Fast topology algorithm for STL files based on half-edges structure[J]. Application of Electronic Technique,2020,46(1):92-95,99.
0 引言
自3D打印技术问世之后,凭借其复杂性低、成本低廉、软件开源、易于推广等特点在国内外得到了迅速的发展[1]。STL(Stereo Lithography)文件是由美国3D System公司于1987年制定的接口协议,由于其格式简单、读写便利,成为3D打印过程中最常用的数据存储格式[2]。STL文件由离散的三角面片组成,存放了模型的点云的位置信息和三角面片的法向量,但其丢失了面与面之间的拓扑关系,同时,单个点被多次记录,造成了大量的数据冗余[3]。在快速成型过程中,待支撑位置查询、模型分层切片等操作均需要三角面间的拓扑关系[4],因此,建立合理的数据结构剔除冗余信息,采用高效的算法建立拓扑关系就显得尤为重要。
针对STL文件读写的局限,国内外专家提出多种解决方案。侯聪聪等[5]提出基于链表的数据存储和拓扑结构,建立点、边、面表进行数据存储,虽剔除了STL文件中的重复点,但每次建立拓扑关系时,均对整个边表进行遍历,算法性能较低;王增波[6]采用哈希表作为基础结构,将有效数据仅保存一次,提升了数据的添加和查找速度,几乎可以在常数时间内快速完成,但建立拓扑关系时,依旧是对已存数据进行遍历,不仅效率较低,还存在部分数据查找遗漏的现象;王彦云等[7]优化了哈希表的冲突解决方案,采用二分查找的方法对相同key值的链表进行查找,提升了查表速度,但拓扑算法效率依旧较低;钱乘等[8]也采用哈希表进行数据存储,存储数据的同时对每个点记录其所属三角面片,全部存储完毕后,再对所有面片进行遍历,建立拓扑关系,不存在遗漏,但读取完成后,需要再次遍历面表寻找邻接面;张应中等[9]利用半边结构进行拓扑关系建立,巧妙地将点与面的信息存入边,利用三角面中顶点的存放顺序来保存边的信息,精简了存储结构,但拓扑算法复杂,并且需要在读入全部顶点的情况下建立拓扑关系。
基于以上算法的研究,本文提出一种基于哈希表的、利用半边结构的数据存储和三角面拓扑算法,在读取数据过程中,一方面剔除冗余数据,一方面快速建立面的拓扑关系,每读入一个三角面信息,进行数据存放的同时,在点表中维护一个未添加邻接面的半边集合。当数据读取完成后,建立无重复数据的点表和面表,完善三角面间的拓扑关系。
1 STL文件
STL格式文件分为ASCII码和二进制两种,其中,二进制格式的文件数据结构如图1所示,与ASCII相比存储更加紧凑,占用空间较小,会在文件起始位置记录三角面片总数Num,在后续建立哈希表时也能依据此选择更加合适的表长。

由欧拉公式可知,存储正确的三角网格文件,三角面的数量约为顶点的2倍[10],而在STL文件中,每存储一次面片信息,都会重复存储3个点的位置坐标,使得存的储顶点数量是面片数量的3倍[11]。由此可得,每个顶点在STL文件中平均记录了6次,所以在进行拓扑关系建立前,需要先对冗余信息进行辨别和剔除,使每个顶点仅存储一次,减少数据存储量,提升算法效率。
2 采用半边结构的拓扑数据结构
2.1 半边的二元组表示
本文采用文献[9]提出的精简半边结构作为基础,使用三角面的标志和半边在面中的序号来表示半边。如图2所示,顶点A、B、C、A按照逆时针顺序连线构成面M1;顶点D、A、C、D连线构成面M2,半边L2可以表示为[M1,2],即M1面中的第2条半边,半边L6可以表示为[M2,3],即M2面中的第3条半边。

当两个半边顶点相同且边的起点与终点相互调换时,两半边互为反向半边,这时,两半边所属三角面互为邻接面。如图2所示,L3和L5为反向半边,M1与M2为邻接三角面。使用二元法表示半边可以精简高效地建立点、边、面的关系,当两半边为反向半边时,可立即得到该半边所在面,从而建立面的拓扑关系。
2.2 拓扑数据结构
基于STL文件的特点和半边二元组的表示,综合考虑空间和效率需求,本文提出如下的基于半边结构的三角面拓扑数据结构。如图3所示,STL文件的几何信息通过顶点和三角面描述,半边信息定义在顶点类中,使用键值对存入Map容器中;临接面信息通过在三角面类中定义一个包含3个元素的数组对其进行存储。

(1)顶点类(Class Vertex)。顶点数据包括顶点位置坐标和一个用来存储半边信息的Map容器。该Map容器以红黑树为底层,存放以该顶点为起点的半边,半边信息通过将上文中的二元组转化为键值对进行存储。使用红黑树作为底层数据结构,可以避免使用连续内存,并将以该点为起点的半边信息全部保存,其搜索时间复杂度为O(lgn),在增加删除半边时,不会对顶点存放的Hash表产生额外影响,同时仍具有较快的速度。
(2)三角面类(Class Mesh)。面数据包含3个指向顶点的指针, 采用一维数组存放,指针存储顺序同时隐性包含了半边顺序,即:顶点V1与V2形成序号为1的半边,顶点V2与V3形成序号为2的半边,顶点V3与V1形成序号为3的半边;此外,将法向量坐标存入normal_vector数组,面片的3个临接面存入border_meshs数组。
2.3 点表和面表
存储顶点数据时,需要快速判断该顶点是否已经保存,鉴于哈希表查找时较低的时间复杂度,采用哈希表对顶点数据进行保存。本文哈希函数如下:

其中,x、y、z为顶点坐标的3个分量值,m为哈希表的长度,h(k)为计算出的哈希地址。由于STL文件数据精度较高,使得各点的值较为接近,因此对k进行一定程度放大。STL文件满足欧拉关系,即三角网格模型的顶点总数是其总三角面片数的1/2,所以m取值为与Num/2最接近的素数,以减少散列地址的冲突。存储顶点的哈希表如图4所示。
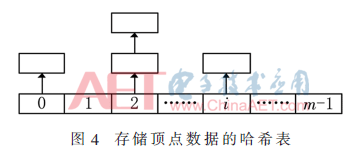
因为面数据不存在重复,所以直接使用面对象数组作为面表,一方面可以在O(1)的时间复杂度内找到对应面片,修改面片信息;另一方面,将数组的下标加1,便可作为面片的标志,可以快速定位半边位置。
3 STL文件拓扑信息重建流程
3.1 冗余信息剔除
当开始进行STL文件读取后,会依次读入所有三角面片的顶点和法向量信息,法向量信息待3个点均读入后存入面对象,将顶点的3个坐标带入式(1)、式(2),计算得到哈希地址,即该点存入点表的位置,而后分为以下两种情况:
(1)若该地址内没有数据,说明该点首次出现,依据该点所在的三角面片的序号和点在面中的位置构建半边,并将其以键值对的形式存入点的half-edges,便完成新点添加。例如,依次读入第4个面片的3个顶点V1、V2、V3,由于V2是第2个读入的点,则构建二元组为[4,2],即第4个面片中的第2个半边,半边方向由V2指向V3。
(2)若该地址存在数据,由于不相同的两点也可能计算出相同的哈希地址,因此需要对比新添加的顶点坐标和已存顶点的坐标是否相同。若相同,则说明该点为重复的旧点,不需要进行添加,进行下一个点的处理;若不同,则该点为新点,同样构建并添加半边信息后,链式添加点解决冲突。例如:读入新点V1,计算得到哈希地址为2,但发现该地址已经存在顶点数据且与V1不同,则需要在该地址处添加指向新点的指针,形成链表来解决哈希地址冲突。
3.2 添加三角面并生成拓扑信息
依次读取并存储3个顶点信息后,依据读取的三角面的序号,更新面表内所对应面的顶点和法向量信息,即vertex数组和 normal_vector数组。第一个面片读取完成后,点表中的半边信息如图5所示,点A、B、C所存半边信息依次为[1,1]、[1,2]、[1,3],即AB、BC、CA半边,此时border_meshs数组内暂无邻接面信息。

后续继续添加面片信息时存在多种情况,以下分别讨论:
(1)新面片的3个顶点与现存顶点均不相同。即3顶点均为第一次读取,构建面数据并将其加入面表后,半边信息如图6所示,其中(A,B,C)为已存面,(D,E,F)为新添加面,所有点目前仅保存一个半边,所有面不存在邻接面。

(2)新面片的3个顶点与现存顶点有一个相同,构建面数据并将其加入面表后,半边信息如图7(a)所示,其中(A,B,C)为已存面,(D,C,E)为新添加面,由于点C不是首次读取,因此点中已经存有指向点A的半边,需将C指向点E的半边也存入其中,即构建[2,2]半边存入点C的half-edges,此时点C中存有两个半边信息,添加后的半边信息如图7(b)所示。此时点C中存有两个半边信息,两个已存面均无邻接面信息。

(3)新面片的3个顶点与现存顶点有两个相同,此时又可分为两种情况,新添加面均为(D,A,C)。①情况1如图8(a)所示,A、C两点为已存点,由于C点已存半边CE与AC半边不是反向半边,因此两面不是邻接面,构建AC、CD两半边分别存入点A、C中即可,此时A、C、E 3点均存有两个半边信息;②情况2如图8(b)所示,A、C两点为已存点,由于C点包含指向A点的半边CA,与新添加面中的AC半边互为反向半边,说明两三角面互为邻接面,向面(A,B,C)的border_meshs数组中添加序号2,向面(D,A,C)的border_meshs数组中添加半边CA所在面序号1,而后删除点C中的半边CA并添加半边CD,即half-edges删除[1,3],添加[2,3],便完成了新面的添加和拓扑关系的建立,此时两面均存在一个邻接面,所有点均包含一个半边。

(4)新面片的3个顶点与现存顶点均相同,此时又可以又可分为4种情况,新加入的面均为(D,A,C)。①情况1如图9(a)所示,不存在新的邻接边,将D、A、C 3点均添加新的半边即可;②情况2如图9(b)所示,有一条新的邻接边,添加DA、CD半边,删除CA半边,并在两面中添加邻接面即可;③情况3如图9(c)所示,有两条新的邻接边,添加DA半边,将CA、DC半边删除,并完善邻接面信息;④情况4如图9(d)所示,3条边均为新的邻接边,将AD、DC、CA半边删除,完善面的邻接信息后即完成面的添加和邻接拓扑信息构建。
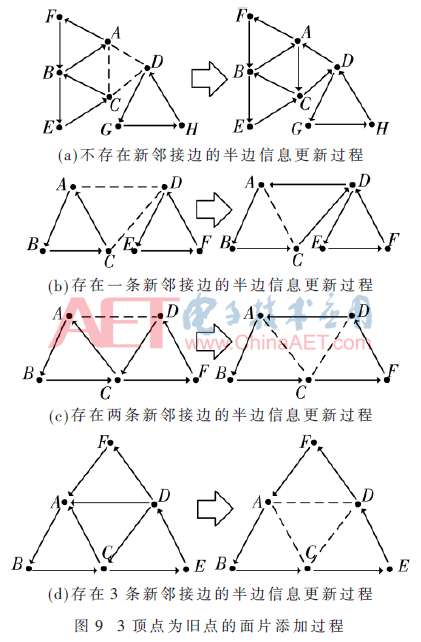
综上,面片的添加与拓补过程与重合点数量相关需分情况讨论。若不存在旧点,则默认构建即可;若存在一个,给该点添加新的半边;若存在两个以上,3点按读入顺序,每两点组成一个新半边,依次判断3个半边的半边,即是否存在新的邻接面。若不存在,则为半边的起点添加新半边;若存在,则在面表内添加新的邻接面,并删除起点的原有半边。注意,若3点中仅有两点为已存点,则需要为删除半边的点添加新的、基于新添加面片的半边(如图8(b)所示)。整个拓扑流程如图10所示。

4 测试实例及性能分析
将上述数据结构和快速拓扑算法通过OpenGL和Qt Creator编程实现,同时,使用文献[8]中的拓扑算法与本文的算法对5个STL模型进行拓扑重建实验,实验环境为Windows 10操作系统,处理器主频为2.6 GHz,4.0 GB内存,获得同一个STL模型在两种算法下的拓扑关系构建时间。表1为两种算法运行时间对比。
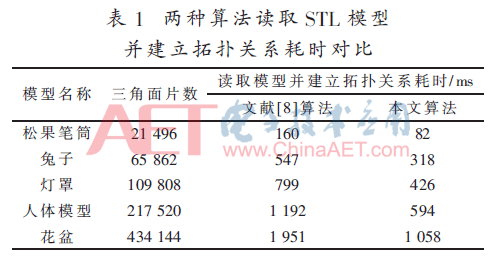
由于本文算法在进行STL文件存储的同时便完成了面片拓扑关系的建立,相比于文献[8]的算法,不需要存储数据后再对面表遍历并进行大量比对寻找邻接面,节省了大量的时间,从测试结果中也可看出本算法具有更高的效率。
5 结论
本文提出半边结构的快速拓扑算法,将半边信息以键值对的形式存入点中,每读入一个面片,存储数据的同时,以较快的效率更新未添加邻接面的半边集合和面表中的邻接面数组,STL模型读取完毕后,面的拓扑信息也同时完善,有效缩短了面片拓扑关系建立的时间,为模型后续的支撑添加和切片处理带来了极大的便利。
参考文献
[1] 宋廷强,邢照合.一种彩色FDM型3D打印机的设计与实现[J].电子技术应用,2017,43(4):69-71,75.
[2] 杨晟院,陈瑶,易飞,等.基于2维流形的STL曲面网格重建算法[J].软件学报,2017,28(12):3358-3366.
[3] 王彦云,陈鸿,谢明师,等.FDM快速成型支撑结构自动生成算法的研究[J].电子技术应用,2015,41(8):146-148.
[4] 徐敬华,盛红升,张树有,等.基于邻接拓扑的流形网格模型层切多连通域构建方法[J].计算机辅助设计与图形学学报,2018,30(1):180-190.
[5] 侯聪聪,南琳,张磊.基于分组的STL模型快速切片算法[J].制造业自动化,2014,36(9):12-15.
[6] 王增波.STL格式文件的快速拓扑重建算法[J].计算机应用,2014,34(9):2720-2724.
[7] 王彦云,陈鸿,谢明师,等.基于哈希表的STL格式文件拓扑重建的算法[J].现代制造工程,2015(12):61-64.
[8] 钱乘,李震,江本赤,等.基于哈希表的STL文件拓扑关系快速重建算法[J].新乡学院学报,2018,35(6):36-39,51.
[9] 张应中,谢馥香,罗晓芳,等.采用半边编码的三角网格拓扑数据结构[J].计算机辅助设计与图形学学报,2016,28(2):328-334.
[10] BOTSCH M,KOBBELT L,PAULY M,et al.Polygon mesh processing[M].Natick:A K Peters,2010:1-2.
[11] 谢馥香.面向三角网格分割体的设计特征重构[D].大连:大连理工大学,2015.
作者信息:
武小超,陈 鸿
(中北大学 仪器与电子学院,山西 太原030051)

