0 引言

    无线传感器网络(Wireless Sensor Networks，WSNs)是一种分布式传感网络。WSNs中的传感器通过无线方式通信，可以与互联网进行有线或无线方式的连接进而形成一个多跳的自组织网络系统^[1]。由于其密集型和随机分布等特点，被广泛应用于环境监测、医疗护理、目标跟踪及交通控制等领域^[2-4]。由于传统传感器节点部署的随机性和盲目性，使传感器对目标区域不能进行有效合理的监测，因此采用合理的传感器部署方案成为WSNs应用中首先要考虑的问题。

    传感器网络优化部署是一个多目标优化问题，一个水质监测系统要实现好的监测效果需要对水质传感器进行合理的部署。目前，国内外许多学者对WSNs的覆盖部署进行了深入的研究，其问题的关键是针对不同的水域情况，通过采用适当的优化策略对特定区域的传感器节点进行部署，在保证传感器覆盖率最大化的条件下，尽可能少地使用传感器，达到资源的有效利用。随着群智能优化算法的兴起，其越来越多地成为研究者关注的焦点。文献[5]-[6]用果蝇算法和鱼群算法对传感器节点进行优化布局，并取得了不错的效果；文献[7]提出了采用加权因子调整的粒子群算法对传感器节点进行自适应部署，但算法中参数值的设定需根据经验值进行设定；文献[8]采用混沌粒子群算法覆盖优化无线传感器网络，该算法的寻优速度较快，但其仍旧没有摆脱粒子群算法易陷入局部极值点的缺点；文献[9]提出了基于改进的蚁群算法优化网络节点，该方法局部搜索能力强，但搜索速度较慢；文献[10]提出了把莱维飞行和粒子群相结合的算法来优化传感器节点，该算法利用莱维飞行搜索的遍历性大大提高了网络的覆盖率，克服了传统粒子群算法容易陷入局部最优的缺点；文献[11]提出分布式布谷鸟算法在无线传感器网络布局优化中的应用，证明了分布式布谷鸟算法在优化时间上要强于粒子群算法，但优化精度不高；文献[12]提出了一种可变参数的改进CS算法，提高了收敛的速度；文献[13]提出了动态适应布谷鸟算法，对布谷鸟的发现概率和搜索步长进行动态调整，使得算法的收敛速度和精度都得到了一定的改善。

    本文布谷鸟算法中用布谷鸟个体作为单个传感器，模拟雏鸟不被寄主发现的过程，将无线传感器网络中覆盖率作为优化目标，布谷鸟优胜劣汰的过程是一个不断迭代，用好的可行解取代较差可行解的过程，因此，在这个过程中可以引入梯度下降求局部最优解的方法。本文通过采用动量梯度下降法、均方根算法、Adam优化算法等深度学习中常用的优化算法的思想，通过更新节点的位置快速计算每次迭代的最优解，能够有效提高问题的优化效率。

1 水质传感器网络覆盖模型

    在水质传感器网络覆盖中，通常通过增加传感器个数以提高覆盖率。然而传感器节点个数过多，会产生大量冗余节点，造成数据传输冲突，影响网络稳定性，且造成资源浪费。因此，在水质传感器网络布局阶段，节点数目和网络覆盖率需要同时考虑。

    本文在监测水域的二维平面内，运用布谷鸟算法对节点自行进行布置，以实现对固定区域内最大覆盖率为目标，在保证监测数据有效的前提条件下，使传感器资源得到进一步的利用。假设每个传感器都有相同的通信半径和感知半径^[14]，设s={s₁，s₂，s₃，…，s_n}是一组无线传感器集合，(x_i，y_i)为集合中任意一个无线传感器节点si的坐标，(x_j，y_j)为监测区域中任意一点p_j的坐标，则节点s_i到点p_j的欧氏距离定义为：

2 算法设计

    布谷鸟搜索(Cuckoo Search，CS)算法是由英国学者Yang于2009年受布谷鸟巢寄生育雏行为的启发提出的一种新型的群智能优化算法。CS算法通过模拟布谷鸟巢寄生育雏行为，结合鸟类、果蝇等的Lévy飞行机制进行寻优操作，能够快速有效地找到问题的最优解。CS算法的关键参数仅为外来鸟蛋被发现的概率和种群数目，整个算法操作简单、易于实现。CS算法利用Lévy飞行进行全局搜索，具有良好的全局寻优能力。

    为了模拟布谷鸟寻窝的方式，需要设定一下3种理性的状态：

    (1)每只布谷鸟每次随机选择一个巢并且产生一个卵；

    (2)在随机选择的一组寄生巢中，最好的寄生巢将会被保留到下一代；

    (3)可利用的寄生巢数量是固定的，寄生巢的主人能发现一个外来鸟蛋的概率为P_a。

    布谷鸟算法中使用D维向量X=[X₁，X₂，…，X_D]表示每一个布谷鸟，结合了全局搜索的随机游走和局部的随机游走，其中，全局搜索的随机游走如式(5)所示：

其中，r是缩放因子，是(0，1)区间内的随机数；X_g，i，X_g，k表示g代的两个随机数。CS算法流程如下：

    (1)初始化种群，用每一个D维向量代表一个巢穴，同时计算出每个个体的适应度。

    (2)更新每个巢穴，按照式(9)产生新的解，产生的新解比原来的解好，则用新解替代旧解。

    (3)对每个巢穴，任选其他两个不一样的巢穴，对D维向量中的每个元素按照式(11)进行组合产生新解，产生的新解比原来的解好，则用新解替代旧解。

    (4)记录整个过程中的最优解，得到的最优解不满足设定的条件时返回步骤（2)，直到满足条件或达到最大迭代次数则返回最优解。

    在布谷鸟算法中影响布谷鸟寻优效率的是Lévy飞行步长控制量的选择和淘汰概率，本文基于深度学习优化算法的思想来更新其参数。

3 基于深度学习的优化算法更新Lévy飞行步长

    在深度学习中，为解决目标函数的最小值，常用梯度下降法进行优化，其基本思想是在每次迭代中，对每个变量，按照目标函数在该变量梯度的相反方向，更新对应的参数值，如式(12)所示：

其中，J(θ)表示损失函数，η表示学习率，其决定了在沿着让目标函数下降最大的方向上，下降的步长有多大。

    本文根据动量梯度下降法(Gradient Descent with Momentum)、均方根算法(Root Mean Square prop)和Adam优化算法(Adam Optimization Algorithm)来更新布谷鸟算法中Lévy飞行的步长。

3.1 动量梯度下降法

    动量梯度下降法的基本思想是计算梯度的指数加权平均数，并利用该梯度更新权重，如式(13)所示：

式中，V_dw是速度更新的大小，β₁是权重，V_t-1是t-1时刻的速度，V_t是当前时刻速度的大小，η是动量梯度下降中的学习率。

    布谷鸟算法中Lévy飞行步长更新采用动量梯度下降法的思想，即每次步长的更新由前一步的步长变化和当前阶段的步长变化共同来决定，如式（14）所示：

其中，Δl是步长更新的大小，Δl_t-1是前一个时刻步长的更新，η是步长更新的学习率。

3.2 均方根算法

    均方根算法的基本思想是在梯度下降中，想缓解纵轴方向的学习率，然后加速横轴方向的学习率，则采用式(15)所示的微分平方的加权平均数，使下降速度变快。

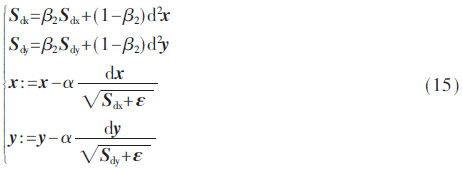
其中，S_dx为x方向上的速度变化，S_dy为 y方向上的速度变化，β₂是均方根中的权重，α是均方根算法中的学习率，ε是一个防止分母为零的十分小的正向量矩阵。通过改变S_dx和S_dy的大小来改变其在某一方向上的寻优速度。

    本文布谷鸟算法中Lévy飞行步长更新采用均方根算法的思想，如式(16)所示：

其中，S_dxy表示循环中每个个体到种群最优位置距离的平均值，X_g是寻优中的每个个体位置，X_best是种群的最优位置。 

3.3 Adam优化算法

    Adam优化算法基本上是将动量梯度下降法和均方根算法结合在一起，且要加上修正偏差。本文布谷鸟算法中Lévy飞行步长更新采用Adam优化算法的思想，如式(17)所示：

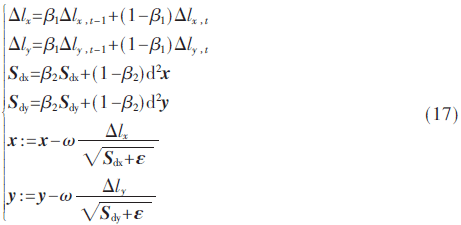
式中，ω为Adam中的学习率。由式(17)可以看出在Adam优化算法中采用了动量梯度下降法的优点，使得在寻优过程中可以跳出局部最优解，同时也吸收了均方根算法的优点，加快了在寻优方向上的搜寻步长，减少了不利的扰动对寻优过程造成的影响。

4 更新淘汰概率P_a

    在梯度下降法寻找最优值的过程中，因为噪音的存在，随着迭代次数的增加，结果会在最优解的附近摆动，不会精确地收敛，此时的学习率是个固定值，因此需要随着迭代次数的增加慢慢减少学习率。

    在本文布谷鸟算法的改进中淘汰概率P_a利用梯度下降的思想，随迭代次数的变化如式(18)所示：

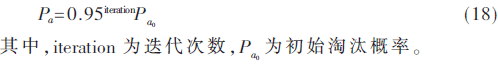
5 仿真结果

5.1 实验设计

    本文采用基于深度学习的优化方法改进布谷鸟算法对传感器节点在监测区域内进行网络覆盖率的最优部署，在100 m×100 m的水域内，以2 m为边长划分网格计算覆盖率。设定传感器半径为10 m，最大迭代次数为1 000，初始淘汰概率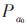设为0.25，β₁设置大小为0.1，β₂设置大小为1，ε设为10^-4，在本文算法中步长控制量以及淘汰概率P_a随迭代次数变化。迭代计算中，当迭代次数大于最大迭代次数时跳出循环，则计算停止，保存最优结果退出布谷鸟更新过程。

5.2 实验结果与分析

    实验中随机生成30个传感器节点，图1为原始的传感器随机分布图，X、Y为二维平面的横纵坐标。由图1可以看出，原始的传感器分布比较杂乱，在随机分配传感器的条件下，其覆盖率比较低,只有59.64%，实际工作中无法达到预期的监测结果。

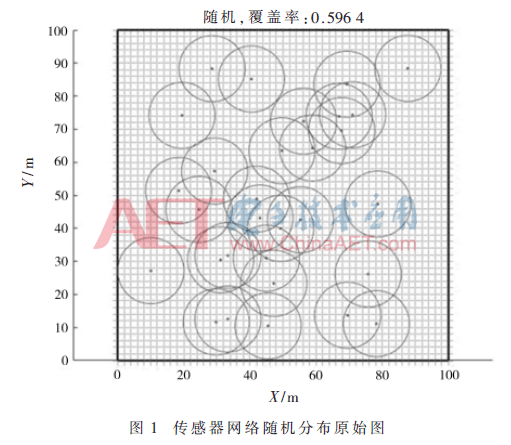
    图2为在随机分布传感器节点的条件下，节点通过基于Adam算法改进的布谷鸟算法Adam-CS迭代更新之后的最优位置分布图，在此分布条件下传感器的覆盖率达到最优。从图2中可以看出，优化后的传感器节点分布比较均匀，传感器的重合度降低，覆盖率达到86.48%，进而使得水质传感器节点部署得到优化，可有效提高传感器网络的监测性能。

    图3为原始布谷鸟算法（CS）、基于动量梯度下降法改进的布谷鸟算法（Momentum-CS）、基于均方根算法改进的布谷鸟算法（RMSprop-CS）以及Adam-CS 4种方法的实验对比图。在相同的区域面积部署相同数量及大小的传感器节点。考虑到随机部署的不确定性对实验结果的影响，对4种方法各进行了10次实验，对实验结果做均值处理。由图3可知，在相同的初始条件下，Adam-CS算法可以更有效地提高网络的部署效果。随着迭代次数的增加，4条曲线趋于平衡，规定每增加30次迭代次数覆盖率增长少于0.05%的情况下为曲线达到的平衡状态，则4种方法的结果如表1所示。可见，Adam-CS算法可以利用更少的迭代次数实现更好的部署效果。

6 结论

    本文基于深度学习的优化方法改进布谷鸟算法，以水质传感器网络覆盖率达到最优为目标，对传感器节点进行优化部署。在充分利用布谷鸟算法优点的基础上，对布谷鸟算法中的步长控制量和淘汰概率利用深度学习的优化方法进行调整，大大提高了算法的寻优性能。仿真结果表明，改进后的算法能高效地搜索全局空间，获得更加精确的结果，实现了深度学习方法和群智能优化算法的结合，同时把改进的算法应用在水质传感器网络的布局优化中，在水环境监测中有一定的实践意义。

参考文献

[1] 毛莺池，陈力军，陈道蓄.无线传感器网络覆盖控制技术研究[J].计算机科学，2007，34(3)：20-22.

[2] PUCCINELLI D，HAENGGI M.Wireless sensor networks:applications and challenges of ubiquitous sensing[J].Circuits & Systems Magazine IEEE，2005，5(3)：19-31.

[3] 徐凯，张秋菊，李克修，等.基于ZigBee的水产养殖无线监控系统设计[J].电子技术应用，2012，38(4)：67-69.

[4] 李建勇，李洋，刘雪梅.基于ZigBee的粮库环境监控系统设计[J].电子技术应用，2016，42(1)：65-67.

[5] 霍慧慧，李国勇.改进的离散果蝇优化算法在WSNs覆盖中的应用[J].传感器与微系统，2016，35(2)：157-160.

[6] 何旭，彭珍瑞，董海棠，等.加权质心鱼群算法在WSNs节点优化布置中的应用[J].传感器与微系统，2018，37(10)：157-160.

[7] 余幸运，孙茜，王小艺，等.基于粒子群优化算法的水质传感器优化部署研究[J].传感器与微系统，2016，35(12)：30-32.

[8] 刘维亭，范洲远.基于混沌粒子群算法的无线传感器网络覆盖优化[J].计算机应用，2011，31(2)：338-340.

[9] 彭丽英.改进的蚁群算法网络节点覆盖优化研究[J].计算机仿真，2011，28(9)：151-153.

[10] 卢玲，谢佳华.莱维飞行的粒子群优化算法在WSNs覆盖增强中的应用[J].传感器与微系统，2015，34(11)：157-160.

[11] 刘小垒，张小松.分布式布谷鸟算法在无线传感器网络布局优化中的应用[J].计算机应用研究，2018，35(7)：2063-2065.

[12] 王稼磊，张会红，汪鹏君，等.基于参数自适应布谷鸟算法的RM电路面积优化[J].计算机应用研究，2018，35(9)：135-137，141.

[13] 明波，黄强，王义民，等.基于改进布谷鸟算法的梯级水库优化调度研究[J].水利学报，2015，46(3)：341-349.

[14] 刘伟，胡安林.无线传感器网络覆盖率与节能性研究[J].电子技术应用，2016，42(6)：98-100.

作者信息:

申志平，孙  茜，王小艺，许继平，张慧妍，王  立

（北京工商大学 计算机与信息工程学院，北京100048）