子阵级LCMV循环优化自适应波束形成算法研究-AET-电子技术应用

子阵级LCMV循环优化自适应波束形成算法研究

2019年电子技术应用第7期

肖宇彤，周渊平，肖骏，周鑫

四川大学电子信息学院，四川成都610065

摘要： 在传统LCMV波束形成器以及子阵空间部分自适应阵的基础上，提出了一种新颖的降维方法。首先将大规模阵列按照子阵划分的某种规则划分为若干组子阵列，每一组子阵列使用相同的权值。在权值优化过程中，每一次只更新权向量的一部分，通过多次迭代更新使系统搜索得到最优权值，避免了全维相关矩阵的求逆运算。实验结果表明，与传统方法相比，该方法在大规模阵列波束形成时能够获得更高的信干噪比，并减小了求逆矩阵的维数，在一定程度上降低了计算复杂度及硬件成本。

关键词： 大规模阵列波束形成 LCMV算法部分自适应阵列循环迭代

中图分类号： TN929.5
文献标识码： A
DOI：10.16157/j.issn.0258-7998.190457
中文引用格式： 肖宇彤，周渊平，肖骏，等. 子阵级LCMV循环优化自适应波束形成算法研究[J].电子技术应用，2019，45(7)：67-71.
英文引用格式： Xiao Yutong，Zhou Yuanping，Xiao Jun，et al. Research on sub-array LCMV cyclic optimization adaptive beamforming algorithm[J]. Application of Electronic Technique，2019，45(7)：67-71.

Research on sub-array LCMV cyclic optimization adaptive beamforming algorithm

Xiao Yutong，Zhou Yuanping，Xiao Jun，Zhou Xin

School of Electronic & Information Engineering，Sichuan University，Chengdu 610065，China

Abstract： In this paper, based on the traditional LCMV beamformer and sub-array space partial adaptive array, a novel dimensionality reduction method is proposed. Firstly, the large-scale array is divided into several groups of sub-arrays according to a certain rule of sub-array division, and each group of sub-arrays uses the same weight. In the process of weight optimization, each time only a part of the weight vector is updated, the system search obtains the optimal weight through multiple iterations, which avoids the inversion of the full-dimensional correlation matrix. The experimental results show that compared with the traditional method, this method can obtain higher signal to interference and noise ratio and reduce the dimensionality of the inversion matrix in large-scale array beamforming, which reduces the computational complexity and hardware cost to a certain extent.

Key words : large scale array；beamforming；LCMV algorithm；partial adaptive array processing；loop iteration

0 引言

自适应波束形成是自适应阵列信号处理的重要分支，广泛应用于无线通信、雷达、语音信号处理等领域^[1]。自适应波束形成问题是在某一准则下寻求最优权矢量，其中包括最小均方(Minimum Mean Squared Error，MMSE)准则、最大信干噪比(Maximum Signal to Interference and Noise Ratio，MSINR)准则、最小噪声方差(Minimum Noise Variance，MNV)准则^[2]。线性约束最小方差(Linearly Constrained Minimum Variance，LCMV)波束形成器是基于MNV的自适应波束形成算法，它在最小方差无失真响应(Minimum Variance Distortionless Response，MVDR)滤波器的基础上引入了线性约束^[3]。但在实际应用中，阵列的阵元数目通常十分庞大，如果使用传统的LCMV算法，全维矩阵求逆的运算量将会变得极其复杂，并且收敛性很差，在工程中难以应用。因此，研究降维方法不仅对理论的发展有重要意义，而且对工程实践也有重要意义^[4]。

本文提出的子阵级LCMV循环优化算法首先对全维阵列进行抽取，形成一组大小不同的子阵列，每组子阵采用相同的权值。在此基础上，再对子阵列进行分块处理，利用循环迭代的思想对权向量进行分块循环优化使其达到收敛。实验结果表明，该方法在大规模阵列波束形成时相较于传统LCMV方法能够获得更高的信干噪比(Signal to Interference and Noise Ratio，SINR)，相较于子阵级LCMV算法能够在达到收敛的基础上进一步减小求逆矩阵的维数，降低计算复杂度及硬件成本。

1 LCMV算法

假设一个M阵元的阵列，X(n)是n时刻M×1维的输入信号向量，C是M×L维的约束矩阵，f是L×1维的约束向量。LCMV算法描述如下：

2 部分自适应阵列处理——子阵级LCMV算法

子阵空间部分自适应阵的结构如图1所示，它是将整个阵列划分为若干个子阵列，每个子阵采用相同的权值进行波束形成^[5]。

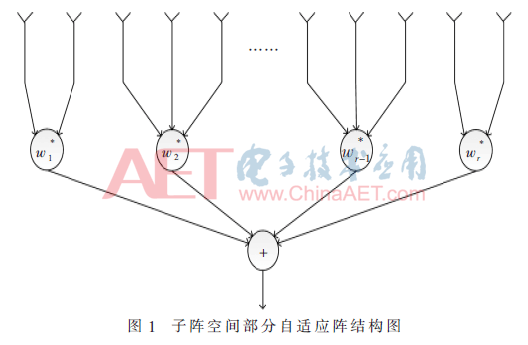
对M阵元均匀线阵进行抽取形成r个子阵，定义降维矩阵T为：

式中，C_T=T^HC是降维后的约束矩阵，维度为r×L。W_T是降维权向量，由于将全阵列抽取为了r个子阵，每个子阵中的阵元共用同一个权值，因此W_T的维数为r×1。

3 子阵级LCMV循环优化算法

将阵列降维输入信号X_T(n)分块为：

式中：

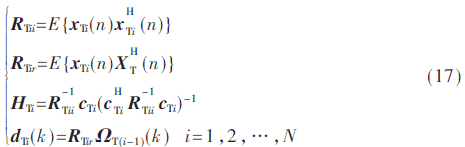
其中，R_Tii是降维输入信号向量分块x_Ti(n)的自相关矩阵。

综上，子阵级LCMV循环优化算法在处理大规模阵列波束形成时的过程如下：

4 仿真分析

4.1 实验1

采用均匀线阵，阵元个数为60，阵元之间的间距为半波长，即d=2/λ。采用子阵级阵列划分，将60个阵元不规则划分为12组，每组的阵元个数依次为：10、6、5、4、4、1、1、4、4、5、6、10。期望信号从0°方向入射，干扰方向为-30°、40°、70°。初始信噪比为10 dB，初始干噪比为10 dB，选取的快拍数为10 000，子阵循环时每个分块大小为2。按照上述参数设置，理想情况下信干噪比SINR=27.781 5 dB。

图2所示是使用LCMV算法形成的波束图，信干噪比SINR=20.868 2 dB。

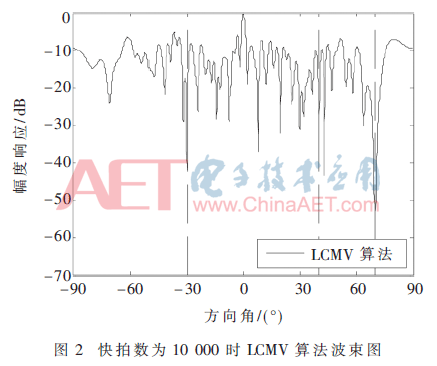
图3虚线所示是子阵级LCMV算法形成的波束图，信干噪比SINR=26.210 5 dB；实线所示是子阵级LCMV循环优化算法形成的波束图, 信干噪比SINR=26.317 0 dB。

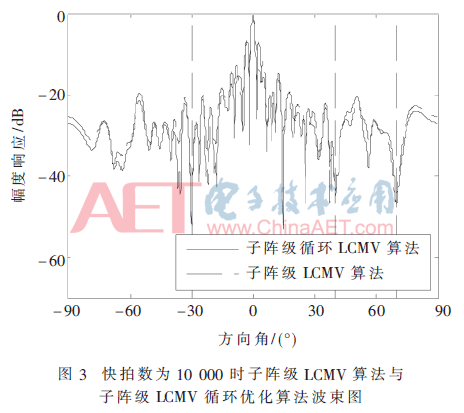
图4是子阵级循环优化的信干噪比收敛曲线图，经过170次循环迭代后权值得到收敛。

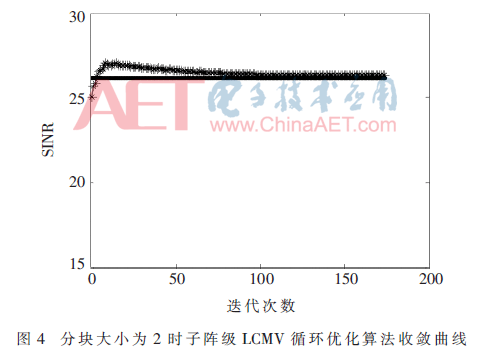
由图2～图4可知，在大规模阵列中，使用LCMV算法得到的波束并不是最佳：收敛性差，旁瓣效应显著且运算量巨大。使用子阵级LCMV算法形成波束时比LCMV算法的SINR高出了约5 dB，干扰得到了有效抑制，且大幅度降低了波束的旁瓣。子阵级LCMV循环优化算法通过循环迭代，波束的SINR收敛于子阵级LCMV算法的SINR，且将输入信号自相关矩阵的维度从60×60降低到2×2。虽然增加了迭代过程，但是大幅度降低了矩阵求逆的运算复杂度，这在实际工程应用中是可行的^[7]。

4.2 实验2

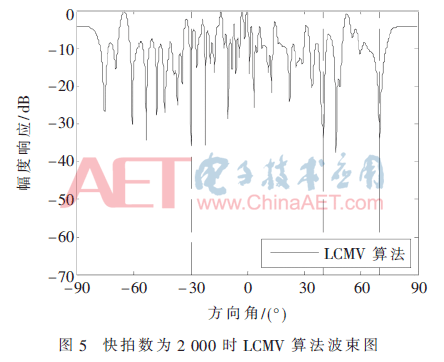
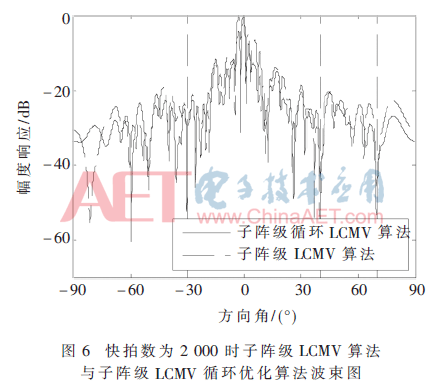
初始参数保持不变，将快拍数减小至2 000，3种算法形成的波束图如图5、图6所示。可知当快拍数减小时，LCMV算法已经无法形成性能良好的波束了，而子阵级LCMV算法与子阵级LCMV循环优化算法能够维持良好的性能，二者的SINR分别为23.639 1 dB、25.482 0 dB。这说明本文所提出的算法能很好地适用于短快拍的应用场景。

4.3 实验3

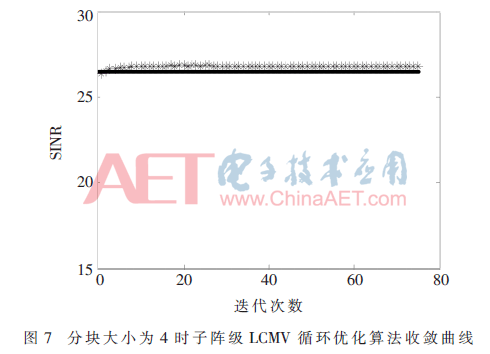
保持实验1中初始参数不变，将分块的大小从2变为4，子阵级LCMV循环优化算法收敛曲线如图7所示。可知，随着分块大小的增加，迭代次数是在不断减小的。

4.4 实验4

为了拓宽主瓣宽度以增加波束的稳健性，在实验1基础上加入高阶导数约束^[8]。图8所示为加入三阶导数约束时，主瓣宽度相较于图3不施加约束时得到了一定展宽，信干噪比为24.175 9 dB。

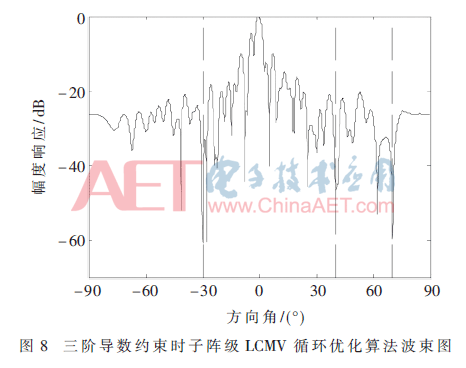
4.5 实验5

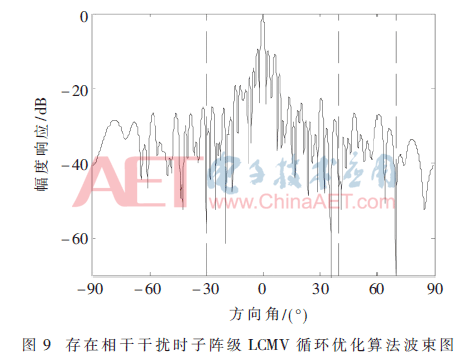
由于在信号传输过程中存在多径，多径在波束形成中属于相干干扰的一种^[9]。此处对子阵级LCMV循环优化算法的相干干扰抑制进行研究。保持实验1中的初始参数不变，将-30°方向处的非相干干扰变为相干干扰，在约束矩阵C中施加相干干扰方向的零点约束，实验结果如图9所示。此时在相干干扰方向形成了很深的零陷，且信干噪比维持在26.997 6 dB。该方法虽然牺牲了一个自由度，但保证了期望信号不会因相干干扰的存在而被对消。

5 结论

针对大规模阵列波束形成问题，本文提出了子阵级LCMV循环优化算法，能够很大程度地降低求逆矩阵的维度，避免了全维矩阵求逆的复杂性。通过实验结果分析，该算法能够在降低维度的同时，形成性能良好的波束，并且在施加导数约束或存在相干干扰时依然适用。这在实际工程应用中降低了大规模相控阵列的计算复杂度和硬件复杂度，具有一定的实用价值。

参考文献

[1] 肖骏，周渊平，肖宇彤.基于CSDM-MIMO系统的虚拟信道估计与权值优化[J].电子技术应用，2019，45(4)：83-86.

[2] 罗俊.认知无线电中基于多天线的信号处理技术的研究[D].武汉：华中师范大学，2017.

[3] 徐峰，孙雨泽，杨小鹏，等.MIMO雷达波束形成的低副瓣LCMV算法[J].信号处理，2017，33(6)：805-810.

[4] YU L，ZHANG X，WEI Y.Adaptive beamforming technique for large-scale arrays with various subarray selections[C].CIE International Conference on Radar.IEEE，2017.

[5] HU X，GUO L，LI S，et al.Improved orthogonal projection adaptive beamforming based on normalization at subarray level[C].IET International Radar Conference 2015.IET，2015.

[6] 王永良，丁前军，李荣锋.自适应阵列处理[M].北京：清华大学出版社，2009.

[7] 刘权，周渊平，徐磊，等.波束形成算法研究与改进[J].信息技术与网络安全，2018，37(4)：92-94，109.

[8] YANG X，SUN Y，LIU Y，et al.Derivative constraint-based householder multistage wiener filter for adaptive beamforming[C].International Radar Conference.IET，2013.

[9] ZHANG L，LIU W.A class of robust adaptive beamforming algorithms for coherent interference suppression[C].Signal Processing Conference.IEEE，2012.

作者信息:

肖宇彤，周渊平，肖骏，周鑫

(四川大学电子信息学院，四川成都610065)

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容